数と式	６　文字式３　（解答）
それぞれ計算しなさい。

１	市立堀川高校 （Ｒ５年）★★	５	城北高校　（R５年）　★★★
が成り立つようなAを求めなさい。 【解】 左辺＝ −8x3y6×4xy×5 ＝ 4 x2y2…ア 125×(−8x2y5) 25 右辺＝A2x2y2 …イ 　ア＝イより, A2＝ 4 で, A＝± 25		A＝3x2＋5xy＋2y2, B＝x2−y2, C＝2x2−xy−3y2 のとき, AC−6B2＝(x＋y)2y×(　　　)である。(　　)にあてはまる式を求めよ。 【解】(x＋y)2が共通因数 A＝(x＋y)(3x＋2ｙ)　B＝(x＋y)(x−y) 　C＝(x＋y)(2x−3y)より, 左辺＝(x＋y)2(3x＋2y)(2x−3y) 　　　　−6(x＋y)2(x−y)2 　＝(x＋y)2{(6x2−5xy−6y2)−6(x2−2xy＋y2)} 　＝(x＋y)2y(7x−12y)で, 7x−12y
２	帝塚山学院泉ヶ丘高校　（Ｒ４年）　★	６	法政大高校　（R５年）　★★
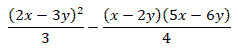【解】 与式＝ 4(4x2−12xy＋9y2)−3(5x2−16xy＋12y2) 3×4 　＝ 16x2−48xy＋36y2−15x2＋48xy−36y2 ＝ x2 12 12		【解】 与式＝ −8a3b6c9×a4b2×9 9ｃ4×4a8b6 　＝ −2a7b8c9 ＝− 2b2c5 a8b6c4 a
３	雲雀丘学園高校　（R４年）　★	７	立命館慶祥高校　（R５年）　★★
【解】 与式＝ (2a−9b)＋2(a＋5b)−4(2a−b) 6 　＝ 2a−9b＋2a＋10b−8a＋4b ＝ −4a＋5b 6 6		【解】 与式＝ −9x3y×25×4y4 10×9x2y4×9 　 　＝ −10x3y5 ＝− 10 xy 9x2y4 9
４	四天王寺高校　（R６年）　★★	８	江戸川学園取手高校　（R６年）　★★
【解】 与式＝ 3(3a−2b)−2(4a＋5b)＋3a＋8b ＝ 4a−8b ＝ a−2b 12 12 3		【解】 与式＝ −a12ｂ6×25×12ab ＝− 12a11 ＝− a11 8 × 9a2b8 × 25 72b 6b

［TOP］　　　［問題にもどる］　　★　中　　★★　やや難　　★★★　難