 
|
 平方数 平方数
112=121 122=144 132=169 142=196
152=225 162=256 172=289 182=324
192=361 252=625 |
 2の累乗 2の累乗
22=4 23=8 24=16 25=32 26=64
27=128 28=256 29=512 210=1024
(2進法でよく使うよ) |
 0の割り算 (0では割れない) 0の割り算 (0では割れない)
0÷1=0
1÷0=解なし (不能)
0÷0=すべての実数 (不定) |
 倍数の見分け方 倍数の見分け方
3の倍数=(各位の数の和)が3の倍数
9の倍数=(各位の数の和)が9の倍数
4の倍数=(下二桁)が4の倍数 |
 3で割ったときの数 3で割ったときの数
3で割り切れる数(3の倍数)=3k (kは整数)
3で割ったとき 1 余る数=3k+1 (kは整数)
3で割ったとき 2 余る数=3k+2 (kは整数)
|
 Nのすべての約数 Nのすべての約数
N=ax×by×cz の約数
| ・ 表し方 … |
(a1〜x) |
× |
(b1〜y) |
× |
(c1〜z) |
| ・ 個 数 … |
x+1個 |
|
y+1個 |
|
z+1個 |
・360(23×32×51)は, 4×3×2=24個の約数がある |
 0と1の約数・倍数 0と1の約数・倍数
・1は,すべての整数の約数
⇒約数に1を入れ忘れるな!
(逆に,すべての整数は1の倍数)
・0は,すべての整数の倍数
⇒倍数に0を入れ忘れるな!
(しかし,どの整数も0の約数ではない) |
 公約数と公倍数 公約数と公倍数
・すべての公約数は,最大公約数の約数
12と18の最大公約数=6
12と18の 全 公約数=1,2,3,6
・すべての公倍数は,最小公倍数の倍数
4と6の最小公倍数=12
4と6の 全 公倍数=12,24,36,48,… |
 連続整数の積 連続整数の積
・連続2整数の積は,2で割り切れる。
(2整数の中に,2の倍数が1つ含まれるから)
5×6 48×49
・連続3整数の積は,3で割り切れる。
(3整数の中に,3の倍数が1つ含まれるから)
5×6×7 48×49×50 |
 比の値 比の値
たとえば
| x |
= |
y |
のとき, |
x |
= |
y |
=k とおき, |
| 2 |
3 |
2 |
3 |
x=2k,y=3k としてみる。
|
 連比 連比
たとえば
| x:y:z=1:2:3 のとき,( |
x |
= |
y |
= |
z |
も同様) |
| 1 |
2 |
3 |
x=k,y=2k,z=3k としてみる。
|
 指数法則 指数法則
xa×xb=xa+b (xa)b=xab
xa÷xb=xa-b (xy)a=xaya
x0=1
・x2×x5=x2+5=x7 ・(x2)3=x2×3=x6
| ・x2÷x5=x2-5=x-3= |
1 |
・(xy)3=x3y3 |
| x3 |
|
 乗法公式 乗法公式
(x+a)(x+b)=x2+(a+b)x+ab
(ax+b)(cx+d)=acx2+(ad+bc)x+bd
(x+y+z)2=(x2+y2+z2)+2(xy+yz+zx)
|
 基本対称式 x+y と xy 基本対称式 x+y と xy
・x2+y2=(x+y)2−2xy
・(x−y)2=(x+y)2−4xy
・x3+y3=(x+y)3−3xy(x+y)
・x2+y2+z2=(x+y+z)2−2(xy+yz+zx) |
 分母が文字の方程式 分母が文字の方程式
| 1 |
+ |
2 |
=5では, X+2Y=5 と置き換え |
| x |
y |
| このとき, |
1 |
=X, |
1 |
=Y としている。 |
| x |
y |
|
 ルートの概数語呂合わせ ルートの概数語呂合わせ
√2=1.414 √3=1.732 √5=2.236
(一夜一夜に人見頃) (人並みにおごれや) (富士山麓オウム鳴く)
√6=2.450 √7=2.645 √10=3.162
(煮よ,良く良く) (菜に虫いない) (三色に並ぶ) |
 分母の有理化 分母の有理化
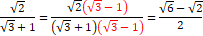
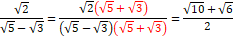
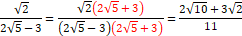 |
 無理数の小数部分 無理数の小数部分
・√5では,2<√5<3だから
(整数部分)=2,(小数部分)=√5−2
・√23では,4<√23<5だから
(整数部分)=4,(小数部分)=√23−4 |
 x=p,qが解となる2次方程式 x=p,qが解となる2次方程式
a(x−p)(x−q)=0 (ただし,a≠0)
したがって,ax2−a(p+q)x+apq=0
・x=−2,3が解となる2次方程式は
a(x+2)(x−3)=0 つまり,ax2−ax−6a=0 |
 解と係数の関係(高校内容) 解と係数の関係(高校内容)
ax2+bx+c=0の解がx=p,qのとき
| 解の和 p+q=− |
b |
,解の積 pq= |
c |
| a |
a |
・x2−3x+1=0では,
解の和 p+q=3,解の積 pq=1 |
 2次方程式の共役な解 2次方程式の共役な解
2次方程式 (係数はすべて有理数) で
x=a+b√cが解なら
もう1つの解は,x=a−b√c
・x=5+√3が解なら,他の解はx=5−√3
| ・x= |
1−2√3 |
が解なら,他の解はx= |
1+2√3 |
| 2 |
2 |
|
 |
x= |
−1+√5 |
が解となる2次方程式 |
| 2 |
両辺を2倍し,移項して,2x+1=√5
両辺を2乗して,4x2+4x+1=5
移項し,4で割ると,x2+x−1=0 |
 二重根号 (a>bのとき) 二重根号 (a>bのとき)
| ・ |
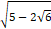 |
= |
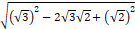 |
=√3−√2 |
|
 自然数の和 自然数の和
・1 〜10の和= 10×11÷2=55
・1〜100の和=100×101÷2=5050 |
 x軸y軸の式・軸に平行な直線 x軸y軸の式・軸に平行な直線
x軸の式は,y=0 y軸の式は,x=0
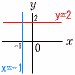
x軸に平行な直線は,y=a
y軸に平行な直線は,x=a |
 対称点の座標 (座標平面上) 対称点の座標 (座標平面上)
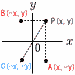
P(x,y)とx軸対称→A( x,−y)
P(x,y)とy軸対称→B(−x, y)
P(x,y)と原点対称→C(−x,−y) |
 比例と反比例 比例と反比例
比例では商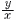 が一定で, が一定で,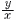 =a(比例定数) =a(比例定数)
よって式は,y=ax グラフは,原点を通る直線
反比例では積xyが一定で,xy=a(比例定数)
よって式は,y=a/x グラフは原点対称の双曲線 |
 変化の割合 (xがp→qのとき) 変化の割合 (xがp→qのとき)
1次関数y=ax+bでは,
変化の割合=a (傾きに等しく,一定)
2次関数y=ax2では,
変化の割合=a(p+q) |
 中点の座標 (座標平面上) 中点の座標 (座標平面上)
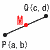 P(a,b)とQ(c,d)の中点Mの座標は P(a,b)とQ(c,d)の中点Mの座標は
・P(1,6)とQ(7,−4)の中点は
|
 2点の距離 (座標平面上) 2点の距離 (座標平面上)
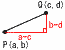 P(a,b)とQ(c,d)の距離は P(a,b)とQ(c,d)の距離は
√(a−c)2+(b−d)2
・P(1,−1)とQ(4,−5)の距離は,
√(1−4)2+(−1+5)2=√9+16=5 |
 直線の式 直線の式
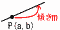 点P(a,b)を通り,傾きmの直線は 点P(a,b)を通り,傾きmの直線は
y=m(x−a)+b
・P(2,3)を通り,傾き−4の直線は
y=−4(x−2)+3で,y=−4x+11
|
 2点を通る直線 2点を通る直線
P(a,b)とQ(c,d)を通る直線は
・P(3,6)とQ(1,−2)を通る直線は
| y= |
6−(−2) |
(x−3)+6で,y=4x−6 |
| 3−1 |
|
 2直線の平行・垂直 2直線の平行・垂直
y=ax+b と y=cx+dが
平行のとき,a=c (傾きは等しい)
垂直のとき,ac=−1 (傾きの積は−1) |
 同一直線上の線分比 (座標平面上) 同一直線上の線分比 (座標平面上)
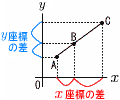
AB:BC
=(AとBのx座標の差):(BとCのx座標の差)
=(AとBのy座標の差):(BとCのy座標の差) |
 等底な三角形の面積の和 (座標平面上) 等底な三角形の面積の和 (座標平面上)
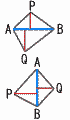
ABが共通底辺のとき,
四角形APBQ=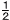 ×AB ×AB
×(PとQのy座標の差)
四角形APBQ=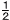 ×AB ×AB
×(PとQのx座標の差) |
 三角形の面積 (座標平面上) 三角形の面積 (座標平面上)
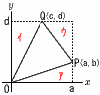
P(a,b),Q(c,d)のとき
| △OPQ= |
ad−bc |
または |
bc−ad |
| 2 |
2 |
△OPQ=ad−(ア+イ+ウ) だから |
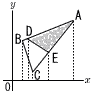  三角形の面積比 (座標平面上) 三角形の面積比 (座標平面上)
(右図参照)
| △ADE |
= |
AD |
× |
AE |
| △ABC |
AB |
AC |
| = |
(AとDのx座標の差) |
× |
(AとEのx座標の差) |
| (AとBのx座標の差) |
(AとCのx座標の差) |
|
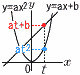  グラフ上の点の座標 グラフ上の点の座標
x座標を t とするとき,
・直線 y=ax+b上の点は (t,at+b)
・放物線 y=ax2上の点は (t,at2) |
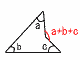
 三角形の外角 三角形の外角
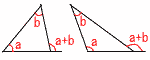
外角=内対角の和
外角と隣り合わない
2つの内角の和に等しい |
 平行線と角 平行線と角
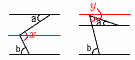
平行な補助線(赤線)を引く
右図で,∠x=∠a+∠b
右図で,∠y=∠b−∠a |
 へこんだ四角形 (くさび形) へこんだ四角形 (くさび形)
へこんだ角は,隣り合わない
他の3つの内角の和に等しい |
 平行線による比 平行線による比
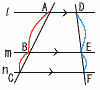
3直線 l,m,n が平行なとき,
AB:BC=DE:EF |
 角の二等分線と比 角の二等分線と比
ADが∠Aの二等分線のとき,
AB:AC=BD:CD |
 等底・等高な三角形は等積 等底・等高な三角形は等積
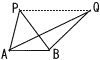 AB(底辺共通), AB(底辺共通),
PQ//AB(等高)
ならば
△PAB=△QAB(等積) |
 等高な三角形の面積比 等高な三角形の面積比
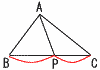 等高な2つの三角形の 等高な2つの三角形の
面積は,底辺の比に比例
△ABP:△ACP=BP:CP |
 等底な2つの三角形の面積比 等底な2つの三角形の面積比
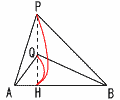
面積は,高さの比に比例
△PAB:△QAB=PH:QH
|
 二等辺三角形の4線 二等辺三角形の4線
| 一致 |
 |
ア 底辺への中線 |
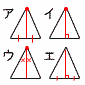 |
| イ 頂点からの垂線 |
| ウ 頂角の二等分線 |
| エ 底辺の垂直二等分線 |
|
 正三角形の4心 正三角形の4心
| 一致 |
 |
ア 外心 |
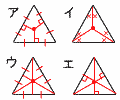 |
| イ 内心 |
| ウ 重心 |
| エ 垂心 |
|
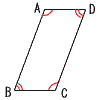  平行四辺形の角 平行四辺形の角
・対角は等しい
∠A=∠C,∠B=∠D
・隣角の和は180°
∠A+∠B=∠C+∠D=180°
∠A+∠D=∠B+∠C=180 |
 中線定理 中線定理
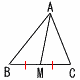
BM=CM(AMが中線)のとき,
AB2+AC2=2(AM2+BM2)
|
 ピタゴラス数 ピタゴラス数
・直角三角形の3辺 (よく出てくる長さ)
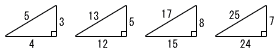
|
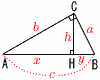  3つの直角三角形 3つの直角三角形
・△ABC∽△ACH∽△CBH
・a:b:c=h:x:b=y:h:a
・ab=ch=2△ABC |
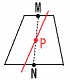  台形の二等分線 台形の二等分線
(上底の中点M)と(下底の中点N)
の中点Pを通る直線で二等分できる |
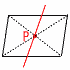  平行四辺形の二等分線 平行四辺形の二等分線
2本の対角線の交点Pを
通る直線で二等分できる |
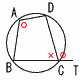  円に内接する四角形(高校内容) 円に内接する四角形(高校内容)
四角形ABCDが円に内接するとき,
・外角=内対角
∠DCT(∠Cの外角)=∠A
・対角の和は180°∠A+∠C=180° |
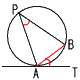  接弦定理(高校内容) 接弦定理(高校内容)
接線と弦のなす角=弦の円周角
∠BAT(接弦角)=∠APB(円周角)
|
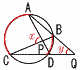  弦のなす角 弦のなす角
∠x=(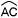 の円周角)+( の円周角)+(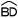 の円周角) の円周角)
∠y=(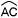 の円周角)−( の円周角)−(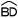 の円周角) の円周角) |
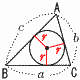  内接円の半径と三角形 内接円の半径と三角形
三角形の面積=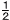 ×(3辺の和)×(半径) ×(3辺の和)×(半径)
△ABC=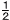 (a+b+c)r (a+b+c)r |
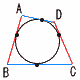  円に外接する四角形(高校内容) 円に外接する四角形(高校内容)
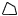 ABCDが円に外接するとき, ABCDが円に外接するとき,
2組の対辺の和は等しい
AB+CD=BC+DA |
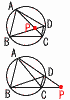  円周上にできる相似三角形 円周上にできる相似三角形
・交点Pが円の内部
△PAB∽△PDC,△PAD∽△PBC
・交点Pが円の外部
△PAB∽△PCD,△PAC∽△PBD |
 平行四辺形の余形 平行四辺形の余形
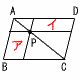 対角線上の点を通って,2辺に平行線を引くと,面積の等しい2つの平行四辺形ができる 対角線上の点を通って,2辺に平行線を引くと,面積の等しい2つの平行四辺形ができる
Pが対角線AC上のとき,  ア= ア=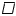 イ イ |
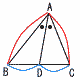
 正三角形の内点からの距離の和 正三角形の内点からの距離の和
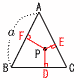
1辺aの正三角形の内点Pと
3辺との距離の和=正三角形の高さ
PD+PE+PF=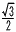 a (△ABCの高さ) a (△ABCの高さ) |
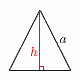  正三角形 正三角形
1辺aの正三角形で
| ・高さは h= |
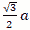 |
| ・面積は S= |
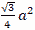 |
|
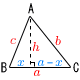  3辺 (a,b,c) から 高さ h を 3辺 (a,b,c) から 高さ h を
h2=c2−x2=b2−(a−x)2より
| ・ |
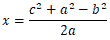 |
で |
| ・ |
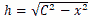 |
|