| 1 |
洛南高校 (R4年) ★ |
5 |
早稲田佐賀高校 (R5年) ★ |
x=−1+√5のとき,
(x−1)x+x(x+1)−(x−2)x
【解】x+1=√5より,2乗して,x2+2x=4
与式=x2−x+x2+x−x2+2x=x2+2x=4 |
a=7.8, b=1.2 のとき, a2+16b2−8ab
【解】
与式=(a−4b)2=(7.8−4×1.2)2
=(7.8−4.8)2=32=9 |
| 2 |
明大付属明治高校 (R5年) ★★ |
6 |
立命館守山高校 (R5年) ★★ |
 |
√2x+√7y=3 …ア |
のとき, y−x |
| √7x−√2y=−6…イ |
【解】ア×√2+イ×√7より, 9x=3√2−6√7 …ウ
ア×√7−イ×√2より, 9y=6√2+3√7 …エ
|
| x+13y=3のとき, |
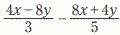 |
【解】
| 与式= |
5(4x−8y)−3(8x+4y) |
= |
−4x−52y |
| 3×5 |
15 |
| = |
−4(x+13y) |
= |
−4×3 |
=− |
4 |
| 15 |
15 |
5 |
|
| 3 |
渋谷教育学園幕張高校(R4年)★★★ |
7 |
東大寺学園高校 (R4年) ★★ |
(1) A=x+y,B=xyとするとき,x4+y4をAとBで
【解】
x2+y2=(x+y)2−2xy=A2−2B
x4+y4=(x2+y2)2−2x2y2=(A2−2B)2−2B2
=A4−4A2B+2B2 |
| x= |
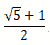 |
,y= |
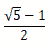 |
のとき, |
3x2−4xy+3y2+x−y
【解】x−y=1, xy=1だから,
与式=3(x−y)2+2xy+(x−y)
=3×1+2×1+1=6 |
| (2) |
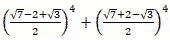 |
の値を求めなさい。 |
| 【解】 |
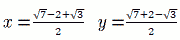 |
と考えると, |
| B=xy= |
(√7)2−(2−√3)2 |
= |
4√3 |
=√3 |
| 2×2 |
4 |
与式=x4+y4=A4−4A2B+2B2
=(√7)4−4(√7)2・√3+2(√3)2
=49−28√3+6=55−28√3 |
8 |
中大杉並高校 (R4年) ★★★ |
| x+y+z=7, xyz=7, |
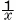 |
+ |
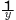 |
+ |
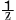 |
= |
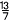 |
のとき, |
【解】
| 与式=1+ |
1 |
+ |
1 |
+ |
1 |
+ |
1 |
+ |
1 |
+ |
1 |
+ |
1 . |
| x |
y |
z |
xy |
yz |
zx |
xyz |
| =1+ |
1 |
+ |
1 |
+ |
1 |
+ |
1 . |
|
+ |
x+y+z |
| x |
y |
z |
xyz |
|
xyz |
|
| 4 |
明大付属明治高校 (R6年) ★★ |
9 |
西大和学園高校 (R6年) ★★ |
x=√1103+√1101, y=√1103−√1101のとき,
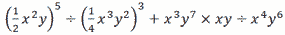
| 【解】与式= |
x10y5×43 |
+ |
x3y7×xy |
= |
2x |
+y2 |
| 25×x9y6 |
x4y6 |
y |
| = |
2(√1103+√1101)2 |
+(√1103−√1101)2 |
| 1103−1101 |
=2(√1103)2+2(√1101)2=4408 |
| x= |
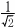 |
,y=√5のとき, |
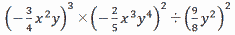
【解】
| 与式= |
−27x6y3×4x6y8×64 |
=− |
4 |
x12y7 |
| 64 × 25 × 81y4 |
75 |
| =− |
4 |
(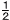 )6(√5)7=− )6(√5)7=− |
5√5 |
| 75 |
48 |
|