| 1 |
大阪府立高校B (R4年) ★ |
7 |
宮城県立高校 (R5年) ★ |
| 等式 b= |
5a+4 |
を aについて解きなさい。 |
| 7 |
【解】両辺×7より, 5a+4=7b
|
等式 4a−9b+3=0 をaについて解きなさい。
【解】移項して, 4a=9b−3
|
| 2 |
弘前学院聖愛高校 (R4年) ★ |
8 |
明治学院東村山高校 (R4年) ★★ |
| 等式 S= |
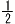 |
h(a+b) をaについて解きなさい。 |
| 【解】 両辺を入れ替えて, |
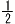 |
h(a+b)=S |
| 移項して, a= |
2S |
−b |
a= |
2S−bh |
も可 |
| h |
h |
|
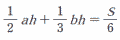 |
を hについて解きなさい。 |
【解】
両辺×6より, 3ah+2bh=S
hでくくり出して, h(3a+2b)=S
| 両辺÷(3a+2b)より, h= |
S . |
| 3a+2b |
|
| 3 |
尚絅学院高校 (R5年) ★ |
9 |
近大附属和歌山高校 (R4年) ★ |
等式 5a+3c=b+6c をcについて解きなさい。
【解】移項して, 3c−6c =b−5a
−3c =b−5a
|
| 等式 a= |
3b−4c |
を cについて解きなさい。 |
| 2 |
【解】両辺×2で,移項して, 4c=3b−2a
|
| 4 |
東北学院高校 (R5年) ★ |
10 |
西大和学園高校 (R4年) ★★ |
| x |
+ |
y |
=1 をyについて解きなさい。 |
| 2 |
3 |
【解】両辺×6より, 3x+2y=6
移項して, 2y=6−3x
| 両辺÷2より, y= |
6−3x |
y=− |
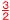 |
x+3 も可 |
| 2 |
|
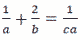 |
を aについて解け。 |
【解】両辺×abcより, bc+2ac=b
移項して, 2ac=b−bc
|
| 5 |
鹿児島育英館高校 (R6年) ★ |
11 |
東海大付属浦安高校 (R6年) ★ |
【解】両辺×5で,移項して,2y=2x−5a
| 両辺÷2より, y= |
2x−5a |
y=x−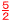 a も可 a も可 |
| 2 |
|
| 等式 a= |
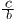 |
+d をcについて解くと, c=( ) |
【解】移項して,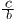 =a−d =a−d
両辺×bより, c=b(a−d) または, c=ab−bd |
| 6 |
桐光学園高校 (R6年) ★★ |
12 |
高知県立高校 (R6年) ★ |
【解】移項して, 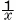 |
= |
y−a |
| ay |
|
1辺がacmの正方形を底面とし,高さがbcmである正四角柱の体積が20cm3であった。このとき,bをaの式で表しなさい。
【解】等式a2b=20を,bについて解く
|