関数	２　比例と反比例２　（略解）

１	岡山白陵高校　（Ｒ５年）　★	５	宮城県立高校　（Ｒ５年）　★
y＋1はx−2に比例し,x＝3のとき,y＝6である。yをxの式で表せ。 【解】 比例定数をaとすると,式はy＋1＝a(x−2)…ア アに(3,6)を代入すると, 6＋1＝a(3−2) 　a＝7で,これをアに代入すると, y＋1＝7(x−2) よって, y＝7x−15		図のように,比例 y＝x…ア のグラフと反比例 y＝…イ のグラフとの交点のうち,x座標が正である点をAとします。点Aのx座標が6のとき,aの値を求めなさい。 【解】点Aのy座標を求める アイにx＝6を代入して,a/6＝×6 　a＝4×6＝24
２	日本大第三高校　（Ｒ４年）　★★	６	関西大倉学園高校　（Ｒ４年）　★★★
yはxに比例し,x＝−4のときy＝−8であり,x＝2＋aのときy＝1＋a2である。このとき,aの値を求めなさい。 【解】 y＝axに(−4,−8)を代入して,−8＝−4a 　a＝2で, 式はy＝2x これに(2＋a, 1＋a2)を代入して, 　1＋a2＝2(2＋a) 　a2−2a−3＝0より, a＝3,−1		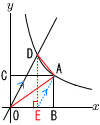図のように,反比例y＝12/x(x＞0)のグラフ上に点A,x軸上に点B,y軸上に点Cをとり,長方形OBACをつくる。また,このグラフと直線y＝2xとの交点をDとする。 (1) 長方形OBACの面積を求めよ。 【解】 A(a,)とすると, 　面積＝a×＝12 (2) 点Dの座標を求めよ。 【解】 ＝2xより, x2＝6 　x＝√6で, D(√6,2√6) (3) 三角形OADの面積が長方形OBACの面積の半分となるときの点Aのx座標を求めよ。 【解】 垂線DEを下ろすと,△OED＝×√6×2√6＝6 このとき,△OED＝OBAC＝6となるから 　平行線EAをとると,△OAD＝△OED＝6 直線EAは,y＝2(x−√6)で, 交点Aは,2(x−√6)＝ 　x2−√6x−6＝0より, x＝(√6＋√30)
３	早稲田実業高等部　（Ｒ４年）　★★
yはx＋2に反比例し,z＋1はyに比例し,x＝4のとき,z＝15である。x＝−6のとき,zの値を求めよ。 【解】 y＝ 　a . …ア　　z＋1＝by …イ x＋2 アをイに代入して, z＋1＝ 　ab . 　…ウ x＋2 　これにx＝4,z＝15を代入して, 16＝ab ab＝96,x＝−6をウに代入して, 　z＝−24−1＝−25
４	新潟県立高校　（Ｒ６年）　★	７	中央大附属高校　（Ｒ６年）　★★
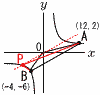電子レンジで食品が温まるまでの時間は,電子レンジの出力に反比例する。ある食品の適切な加熱時間が500Wの出力で3分のとき,600Wの出力での適切な加熱時間は何分何秒か,答えなさい。 【解】 出力をxW,時間をy分とすると, 反比例だから，y＝に(500,3)を代入して, 　3＝a/500で,比例定数はa＝1500 y＝1500/xに,x＝600を代入して, 　y＝1500/600＝＝2分30秒		関数y＝のグラフ上に点Ａ,Ｂがあり,x座標はそれぞれ12,−4である。原点をOとするとき,△OＡＢと△ＰＡＢの面積が等しくなるように点Ｐを関数y＝のグラフ上にとる。このとき,点Ｐの座標を求めなさい。ただし,点Ｐのx座標は−4より小さいものとする。 【解】(右図参照) A(12,2), B(−4,−6)で,ABの傾きは Oを通り,ABに平行な直線はy＝x 交点Pは,＝xより,x2＝48 よって, P(−4√3,−2√3)

［TOP］　［問題にもどる］　　★　中　　★★　やや難　　★★★　難