 関数 |
７ グラフの利用１ （略解） | |
| １ | 兵庫県立高校 （Ｒ４年） ★★ | ２ | 盈進高校 （Ｒ５年） ★★ | ||||||||||||||
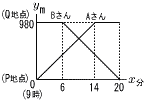 (1) Aさんは分速何mで歩いたか【解】 980mを14分で歩いたから, 980÷14＝70m/分 (2) Bさんについて,yをxの式で表しなさい。 【解】 y＝ax＋bに,(6,980)と(20,0)を代入して,
(3) すれちがったのは,P地点から何mの地点か 【解】 Aの式は, y＝70x …イ アイより,−70x＋1400＝70xで, x＝10 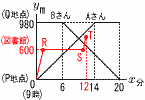 y＝70×10＝700m(4) Cさんが図書館にいた時間は何分何秒か 【解】(右上図参照) 図書館にt分いたとすると, R(2,600) S(2＋t,600) 9時12分に,Aは840m地点,Bは560ｍ地点だから, Cは(840＋560)÷2＝700m地点で,T(12,700)
|
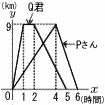 次のグラフは,9km離れた2地点A,B間をPさんとQ君がA地点を同時に出発して往復した様子を示したものである。xはPさんとQ君がA地点を出発してからの時間を,yはA地点からの道のりを表している。(1) PさんがA地点を出発してB地点に着くまでのxとyの関係式を求めなさい。 【解】原点を通る直線 y＝axに(4,9)を代入して, 9＝4aで,a＝  式は, y＝  x …ア(2) Q君が,B地点からA地点にもどるときの速さは毎時何kmですか。また,この間のxとyの関係式を求めなさい。 【解】(2,9)と(5,0)を通る直線 9kmを3時間だから,9÷3＝3kmで,毎時3km y＝−3x＋bに(5,0)を代入して, 0＝−15＋b b＝15で, 式は y＝−3x＋15 …イ (3) Q君は,B地点からA地点にもどる途中,Pさんと出会いました。その地点は,B地点から道のりが何kmの地点かを答えなさい。 【解】出会い地点はアとイの交点 ア＝イより, x＝−3x＋15で,x＝ これをアに代入して,y＝ ×＝45/7Bからの道のり＝9−(45/7)＝18/7km |
||||||||||||||||
| ３ | 熊本県立高校 （Ｒ５年） ★ | ４ | 慶應義塾高校 （Ｒ６年） ★★★ | ||||||||||||||
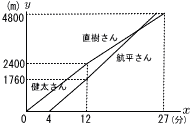 健太さんと直樹さんは,航平さんと,運動公園にある１周2400mのジョギングコ−スを走った。3人ともスタート地点から同じ方向に一定の速さで走り,健太さんと直樹さんは,健太さんから直樹さんの順にそれぞれ１周ずつ,航平さんは一人で2周走った。(1) 航平さんの走る速さは毎分何ｍか,求めなさい。 【解】1760mを8分 1760÷(12−4)＝200 毎分220ｍ (2) 航平さんが直樹さんと並んだのは,健太さんが走り始めてから何分何秒後か,求めなさい。 【解】2直線の交点 ・直樹の式は,2点(12,2400)と(27,4800)を通る から, y＝160x＋480 …ア ・航平の式は,傾き220で,(4,0)を通るから, y＝220x−880 …イ ア＝イより,x＝  で, 22分40秒後 |
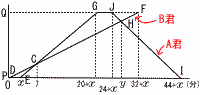 A君はP地点を出発してから20分後にQ地点に到着し,そこで4分間休憩した後に再び20分かけてP地点に戻ってきた。B君はA君より数分早くP地点を出発し,出発してから7分後にA君に追い抜かれ,A君がQ地点を出発してから8分後にQ地点に到着した。(1) A君がP地点を出発したのは,B君が出発してから何分後か。 【解】(右図参照) B君出発のx分後にA君が出発したとすると, グラフで,△CDE∽△CFGより,CD:CF＝DE:FG 7:{(32＋x)−7}＝x:(4＋8) これを解いて, x＝3分後 (2) A君がQ地点を出発した後にB君とすれ違うのは,B君がP地点を出発してから何分後か。 【解】 B君出発のy分後にすれ違ったとすると, グラフで,△HDI∽△HFJより,HD:HF＝DI:FJ y:{(32＋3)−y}＝(44＋3):8 これを解いて, y＝329/11分後 |
||||||||||||||||
