関数	８　グラフの利用２　（略解）

１	秋田県立高校　（Ｒ５年）　★	３	常盤高校　（Ｒ４年）　★★
駅から3600ｍ離れた図書館まで,まっすぐで平らな道がある。健司さんは,午前10時に駅を出発し,毎分60ｍの速さで図書館に歩いて向かった。駅から1800ｍ離れた地点で立ち止まって休憩し,休憩後は毎分120ｍの速さで図書館に走って向かい,午前10時50分に図書館に着いた。 　次の図は,健司さんが駅を出発してからx分後に,駅からyｍ離れた地点にいるとして,xとyの関係を表したグラフの一部である。 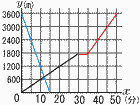(1) 健司さんが駅から1800ｍ離れた地点で休憩を始めてから,図書館に着くまでのxとyの関係を表したグラフを,図にかき加えなさい。 【解】右図の赤線 (3600−1800)÷120＝15分で,休憩は5分 (2) 健司さんの姉の美咲さんは,健司さんが駅を出発した時刻と同じ時刻に,自転車に乗って図書館を出発し,毎分240ｍの速さで駅に向かっていたところ,歩いて図書館に向かう健司さんと出会った。美咲さんと健司さんが出会ったときの時刻は,午前10時（　　）分である。 【解】10時x分に出会ったとすると, 健司さんの式は,y＝60x(青直線) …ア 美咲さんの式は,y＝−240x＋3600 …イ ア＝イより,x＝12　　午前10時12分		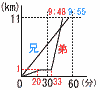兄と弟が,ある日曜日の朝,午前9時に家を出発し,同じ道を通って家から11km離れた遊園地に向かった。 　兄は自転車に乗り時速12kmで進み,弟は家から1km離れたバス停まで時速3kmで歩き,そこで13分待ち,バスに15分間乗って遊園地に着いた。 　右の図は,兄と弟が家を出発してから遊園地に着くまでの時間と道のりを表しているものである。 (1) 兄は20分後に家から何kmの地点にいるか。 【解】20分＝時間 12×＝4km (2) 家を出発してから35分後に,兄と弟の間の距離は何km離れているか。 【解】バスの式は,(33,1) (48,11)を通る直線 弟(ﾊﾞｽ)の式は,y＝x−21…ア 　x＝35を代入して,y＝ 兄の式は,y＝x…イ 　x＝35を代入して,y＝7 よって,7−＝14/3km (3) 弟が乗ったバスが兄の自転車に追いついたのは家から何kmの地点か。 【解】交点のy座標を求める イよりx＝5yで,これをアに代入すると, 　y＝×5y−21　よって, y＝9km
２	愛媛県立高校　（Ｒ５年）　★	４	関西学院高等部　（Ｒ６年）　★★★
太郎さんは,午哨9時ちょうどに学杖を出発して,図書館に向かった。学校から図書館までは一本道であり,その途中に公園がある。 (1) 太郎さんが公園に到着したのは午前何時何分か求めよ。 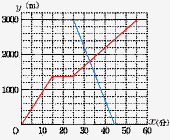【解】 1200÷80＝15分で, 　午前9時15分 (2) 太郎さんか学校を出発してからx分後の学校からの道のりをyｍとするとき,太郎さんが学校を出発してから図書館に到着するまでのxとyの関係を表すグラフをかけ。 【解】右図の赤線 後半は,1800÷60＝30分 (3) 花子さんは,午前9時20分ちょうどに図書館を出発し,一定の速さで走って学校へ向かった。途中で太郎さんと出会い,午前9時45分ちょうどに学校に到着した。花子さんが太郎さんと出会ったのは午前何時何分何秒か求めよ。(右へ続く→)		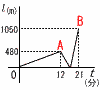兄と弟が同時に自宅を出発し,異なる速さで駅までの一直線の道を進んだ。駅に向かっている途中に兄は忘れ物をしたことに気付き,それまでの1.1倍の速さで来た道を引き返した。右のグラフにおいて,縦軸は弟が駅に着くまでの兄弟間の距離l (ｍ)を表しており,横軸は2人が自宅を出発してからの時間t (分)を表している。このとき,弟の道を進む速さは毎分何ｍか求めよ。ただし,道を進む速さは兄の方が弟よりも速いものとする。 【解】速さを,兄xm/分,弟ym/分とすると, A地点で,12(x−y)＝480…ア B地点で,21y−(12x−1.1x×9)＝1050…イ アイを連立させて解くと,x＝100, 弟はy＝60m/分
		(左の解答つづき) 【解】グラフの交点を求める 太郎(後半)の式はy＝60x−300…ア 花子の式は,,y＝−120x＋5400…イ ア＝イより,x＝31で, 午前9時31分40秒

［TOP］　［問題に戻る］　　★　中　　★★　やや難　　★★★　難