 関数 |
１１ 変域２ （略解） | |
| 関数 |
１１ 変域２ （略解） | |
| １ | 日本大第三高校 （Ｒ５年） ★★ | ５ | 慶應義塾高校 （Ｒ５年） ★ | |||
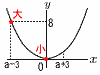 関数y＝ x2について,xの変域がa－3≦x≦a＋3のとき,yの変域はb≦y≦8である。定数a,bの値をそれぞれ求めなさい。ただし,－3＜a＜0とする。【解】(右図参照）下に凸の放物線 －3＜a＜0より,xの変域は0を含むから, 最小値 x＝0のとき, b＝ ×02より, b＝0|a＋3|＜|a－3|だから,最大値はx＝a－3のとき, 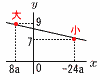(a－3)2＝8で, a＝－1 |
 a,bを定数とする。1次関数y＝ax＋bついて,xの変域が8a≦x≦－24aのとき,yの変域が7≦y≦9であったという。このとき,a＝( ), b＝（ ）である。【解】(右図参照） 8a≦－24aより,a＜0で,右下がりの直線 y＝ax＋bに,(8a,9)と(－24a,7)を代入して, 8a2＋b＝9…ア －24a2＋b＝7…イ アイを連立させて解くと, a＝－  b＝17/2 |
|||||
| ２ | 東洋大京北高校 （Ｒ４年） ★★ | ６ | 近大附属高校 （Ｒ４年） ★★★ | |||
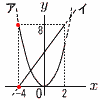 xの変域が－4≦x≦2のとき,2つの関数y＝x2…アとy＝ax＋b(a＞0)…イのyの変域が一 致します。このとき,a,bの値を求めなさい。【解】(右図参照）イは右上がりの直線 アの変域は,0≦y≦8 イの変域は,－4a＋b≦y≦2a＋b
 b＝ |
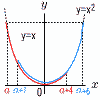 関数y＝x2において,xの変域がa≦x≦a＋4…アのときのyの変域と,xの変域がa＋1≦x≦a＋6…イのときのyの変域が一致する。このとき,aの値を求めよ。【解】(右図参照）下に凸の放物線 アイともに最小値はy＝0 アの最大値は,x＝aのときで,y＝a2 イの最大値は,x＝a＋6のときで,y＝(a＋6)2 最大値も一致するから,a2＝(a＋6)2 12a＋36＝0で, a＝－3 |
|||||
| ３ | 國學院大久我山高校 （Ｒ４年） ★★ | ７ | 立教新座高校 （Ｒ４年） ★★★ | |||
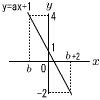 関数y＝ax＋1(a＜0)のxの変域がb≦x≦b＋2のとき,yの変域は－2≦y≦4となる。このとき,a＝[ ], b＝[ ]である。 【解】(右図参照）右下がりの直線 最小値はx＝b＋2のとき,y＝a(b＋2)＋1＝－2 ab＋2a＝－3…ア 最大値はx＝bのとき,y＝ab＋1＝4 ab＝3…イ アイより, a＝－3，b＝－1 |
関数y＝ax2について,xの変域が－6≦x≦3…アのとき,yの変域は0≦y≦24です。また,xの変域がb≦x≦3…イのとき,yの変域は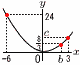 ≦y≦cです。このとき,定数a,b,cの値を求めなさい。 【解】(右図参照）アのとき,最大値はx＝－6のとき, y＝(－6)2a＝36a＝24で, a＝  イのとき,最小値はx＝bのとき, y＝  b2＝で, b＝±2b＝－2なら最小値は にならない b＝2イのとき,最大値はx＝3のときで,y＝ ×32＝cで,c＝6 |
|||||
| ４ | 国学院大久我山高校 （Ｒ６年） ★★ | ８ | 大阪府立高校Ｃ （Ｒ６年） ★★ | |||
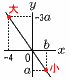 1次関数y＝－3x＋bにおいて,xの変域が－4≦x≦bのとき,yの変域はa≦y≦－3aである。このとき, a＝（ ）,b＝（ ）である。【解】(右図参照）右下がりの直線 最小値はx＝bのとき,y＝－3b＋b＝a…ア 最大値はx＝－4のとき,y＝－3×(－4)＋b＝－3a…イ アイを連立させて解くと, a＝－24/5, b＝12/5 |
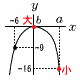 a,bを定数とする。関数y＝－ x2について,xの変域が－6≦x≦aのときのyの変域が－16≦y≦bであるとき,a,bの値をそれぞれ求めなさい。【解】(右図参照）上に凸の放物線 最小値はx＝aのとき,y＝－ a2＝－16で, a＝8最大値は原点で, b＝0 |
|||||
