| 1 |
石川県立高校 (R4年) ★ |
5 |
青雲高校 (R6年) ★ |
関数y=x2についてxの値がaからa+3まで増加するときの変化の割合が13である。このときのaの値を求めなさい。
【解】
| 変化の割合= |
(a+3)2-a2 |
=13 |
| (a+3)-a |
| 6a+9 |
=13より, 6a+9=39で,a=5 |
| 3 |
|
反比例を表す関数y=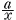 のグラフが点(-3,4)を通る。この関数について,xの値が2から4まで増加するときの変化の割合を求めよ。 のグラフが点(-3,4)を通る。この関数について,xの値が2から4まで増加するときの変化の割合を求めよ。
【解】y=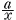 に(-3,4)を代入して,a=-12 に(-3,4)を代入して,a=-12
x=2のとき,y=-12/2=-6
x=4のとき,y=-12/4=-3
| 変化の割合= |
(-3)-(-6) |
= |
3 |
| 4-2 |
2 |
|
| 2 |
就実高校 (R4年) ★★ |
6 |
新潟県立高校 (R6年) ★★ |
xの値がa-2からa+4まで増加するとき,1次関数y=-x+1…ア と関数y=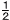 x2…イ の変化の割合が等しくなった。このとき,a=[ ]である。 x2…イ の変化の割合が等しくなった。このとき,a=[ ]である。
【解】
アの変化の割合=傾き=-1
| イの変化の割合= |
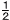 (a+4)2- (a+4)2-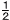 (a-2)2 (a-2)2 |
=a+1 |
| (a+4)-(a-2) |
a+1=-1より, a=-2 |
関数y=ax2について,xの値が1から4まで増加するときの変化の割合が2a2である。このとき,aの値を求めなさい。ただし,a≠0とする。
【解】
| 変化の割合= |
42a-12a |
= |
16a-a |
=5a |
| 4-1 |
3 |
5a=2a2より, a=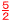
|
| 3 |
中央大附属横浜高校 (R5年) ★ |
7 |
県立岡山朝日高校 (R6年) ★★ |
yがxに反比例していて,x=2のとき,y=3である。xの値が-6から-2まで増加するときの変化の割合を求めなさい。
【解】y=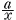 に(2,3)を代入して, に(2,3)を代入して,
3=a/2より,a=6で,反比例の式はy=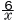
| 変化の割合= |
(-3)-(-1) |
= |
-2 |
=-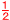 |
| (-2)-(-6) |
4 |
|
関数y=ax2について,xの値が-4から2まで増加するときの変化の割合が3であった。この関数について,xの値が3から7まで増加するときの変化の割合は[ ]である。
【解】
| 割合(-4~2)= |
22a-(-4)2a |
= |
-12a2 |
=3で, a=-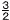 |
| 2-(-4) |
6 |
| 割合(3~7)= |
-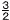 ・72-(- ・72-(-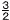 )・32 )・32 |
= |
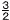 (-49+9) (-49+9) |
=-15 |
| 7-3 |
4 |
|
| 4 |
成城学園高校 (R6年) ★★ |
8 |
芝浦工大附属高校 (R6年) ★★ |
xの値が−1から3まで増加するとき,2つの関数y=ax2…アとy=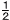 x+3…イの変化の割合が等しい。このとき定数aの値を求めよ。 x+3…イの変化の割合が等しい。このとき定数aの値を求めよ。
【解】
| アの変化の割合= |
32a-(-1)2a |
= |
9a-a |
=2a…ウ |
| 3-(-1) |
3+1 |
| イの変化の割合= |
(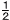 ×3+3)-{ ×3+3)-{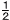 ×(-1)+3} ×(-1)+3} |
= |
2 |
=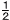 …エ …エ |
| 3-(-1) |
4 |
ウ=エより, 2a=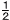 で, a= で, a=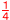 |
ある斜面を球が転がり始めてからx秒間に転がる距離をymとすると,yはxの2乗に比例する。球は,転がり始めて4秒間で24m転がった。このとき,球が転がり始めて3秒後から7秒後までの間の平均の速さを求めなさい。
【解】y=ax2に,(4,24)を代入すると,
24=42aで,a=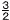
| 変化の割合= |
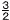 ×72- ×72-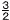 ×32 ×32 |
= |
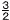 (49-9) (49-9) |
=15m/秒 |
| 7-3 |
4 |
|