| 1 |
明学東村山高校 (R6年) ★ |
5 |
江戸川学園取手高校 (R6年) ★ |
2次関数y=−x2において,xの値が−3 から 4 まで増加するとき の変化の割合を求めなさい。
【解】
| 変化の割合= |
−42−{−(−3)2} |
= |
−16+9 |
= |
=−1 |
| 4−(−3) |
4+3 |
|
関数y=\(\sqrt{x}\)について,xの値が4から9まで増加するときの変化の割合を求めなさい。
【解】
| 変化の割合= |
√9−√4 |
= |
3−2 |
= |
1 |
| 9−4 |
5 |
5 |
|
| 2 |
東京工大附属科技高校 (R4年) ★ |
6 |
桐光学園高校 (R5年) ★★ |
関数y=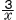 で,xの値が で,xの値が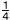 から から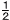 まで増加するときの変化の割合を求めなさい。 まで増加するときの変化の割合を求めなさい。
【解】
x=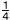 のとき,y=3÷ のとき,y=3÷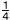 =12 =12
x=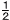 のとき,y=3÷ のとき,y=3÷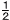 =6 =6
|
1次関数y=−4x+2…ア と2次関数y=2x2…イ において,xの値がaからa+3まで増加ときの変化の割合が等しいとき,定教aの値を求めよ。
【解】
アの変化の割合=傾き=−4
| イの変化の割合= |
2(a+3)2−2a2 |
| (a+3)−a |
4a+6=−4より, a=−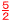 |
| 3 |
国立高専 (R5年) ★ |
7 |
城北高校 (R6年) ★ |
2つの関数y=ax2…ア とy=−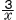 …イ について,xの値が1から3まで増加するときの変化の割合が等しいとき,a=( )である。 …イ について,xの値が1から3まで増加するときの変化の割合が等しいとき,a=( )である。
【解】
| イの変化の割合= |
(−1)−(−3) |
=1 |
| 3−1 |
4a=1より, a=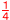 |
2つの関数y=x2…ア,y=2x…イにおいて,xの値がtからt+3まで変化するときの変化の割合は等しい。このとき,定数tの値を求めよ。
【解】
| アの変化の割合= |
(t+3)2−t2 |
= |
6t+9 |
=2t+3…ウ |
| (t+3)−t |
3 |
| イの変化の割合= |
2(t+3)−2t |
= |
6 |
=2…エ |
| (t+3)−t |
3 |
ウ=エより,2t+3=2で, t=−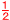 |
| 4 |
明治大付属八王子高校 (R6年) ★★ |
8 |
東京工大附属科技高校 (R6年) ★★ |
関数y=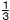 x2について,xがaからa+4まで増加したときの変化の割合は x2について,xがaからa+4まで増加したときの変化の割合は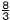 です。aの値を求めなさい。 です。aの値を求めなさい。
【解】
| 変化の割合= |
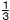 (a+4)2− (a+4)2−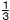 a2 a2 |
= |
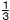 (8a+16) (8a+16) |
=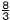 |
| (a+4)−a |
4 |
2a+4=8で, a=2
|
高いところから物を落とすとき,落ち始めてからx秒間に落ちる距離をymとすると,y=4.9x2の関係が成り立っている。落ち始めてから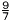 秒後から 秒後から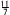 秒後までの間の平均の凍さは,秒速何mかを求めなさい。 秒後までの間の平均の凍さは,秒速何mかを求めなさい。
【解】
| 変化の割合= |
4.9(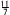 )2−4.9( )2−4.9(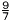 )2 )2 |
=4.9×(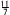 + +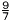 )=14m/秒 )=14m/秒 |
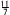 − −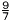 |
|