| 14 放物線と直線1 (略解) | ||
| 14 放物線と直線1 (略解) | ||
| 1 | 法政大高校 (R4年) ★★ | 4 | 山梨県立高校 (R5年) ★ | ||||
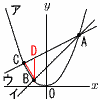 図のように放物線y=ax2…ア と,直線y=x+4…イ は2点A,Bで,直線y= 図のように放物線y=ax2…ア と,直線y=x+4…イ は2点A,Bで,直線y=(1) aの値を求めなさい。 【解】 イウよりx+4= これをアに代入して,42a=8より, a= (2) △ABCの面積を求めなさい。 【解】B(-2,2) C(-3, ウにx=-2を代入して, D(-2,5) △ABC= |
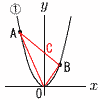 ①は関数y=ax2(a>0)のグラフであり,点A,Bは①上にある。点A,Bのx座標はそれぞれ-6,4である。 ①は関数y=ax2(a>0)のグラフであり,点A,Bは①上にある。点A,Bのx座標はそれぞれ-6,4である。(1) a= 【解】y= A(-6,9)とB(4,4)を通るから
【解】A(-6,36a) B(4,16a) ABはy=-2ax+24a △AOB= = |
||||||
| 2 | 久留米大附設高校 (R5年) ★★★ | 5 | 近畿大附属高校 (R5年) ★★ | ||||
放物線y=x2…ア と直線y=x+6…イ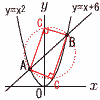 (1) A,Bの座標をそれぞれ求めよ。 (1) A,Bの座標をそれぞれ求めよ。【解】x2=x+6より,x=-2,3 A(-2,4) B(3,9) (2) Cのy座標をすべて求めよ。 【解】C(0,c)とすると, AC2=(0+2)2+(c-4)2=c2-8c+20…ウ BC2=(0-3)2+(c-9)2=c2-18c+90…エ AB2=(-2-3)2+(4-9)2=50…オ △ABCは直角三角形だから,ウ+エ=オ c2-13c+30=0より, y=3,10 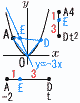 (3) △OAE:△ODE=1:3のとき,tの値 (3) △OAE:△ODE=1:3のとき,tの値【解】AE:ED=1:3 Eのx座標=t- Eのy座標=4- キクをカに代入して, t2+3t-6=0で, t=(-3+√33)/2 |
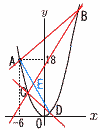 放物線y=ax2…①がある。 放物線y=ax2…①がある。①は点A(-6,18)を通る。 (1) aの値を求めよ。 【解】①に(-6,18)を代入して, 18=(-6)2aで, a= (2) 直線ABの式を求めよ。 【解】y=(x+6)+18で, y=x+24 …ア (3) 直線CDの式を求めよ,I, 【解】 直線CBはy=2(x-8)+32=2x+16…イ 直線CDはy=-(x+4)+8で, y=-x+4 (4) 面積比△ABD:△ACDを求めよ。 【解】ADとBCの交点E(- 底辺ADが共通だから,△ABD:△ACD=BE:EC y座標を比較すると,(32-11):(11-8)= 7:1 |
||||||
| 3 | 法政大第二高校 (R6年) ★★ | 6 | 早稲田実業高等部 (R6年) ★★★ | ||||
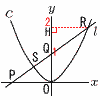 放物線C:y=x2…アと直線l:y=ax+1…イがある。PQ=QRのとき, 放物線C:y=x2…アと直線l:y=ax+1…イがある。PQ=QRのとき,(1) 点Rのy座標を求めなさい。 【解】Rからy軸に垂線RHを下ろすと, △QHR≡△QOPより,QH=1で, y=2 (2) aの値を求めなさい。 【解】アにt=2を代入して,R(√2,2) これをイに代入して,2=√2a+1より, a=√2/2 (3) RSの長さを求めなさい。 【解】イをアに代入して, 2x2-√2x-2=0より,x=√2,- R(√2,2),S(- |
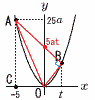 放物線y=ax2(a>0)上に2点A,Bがある。 放物線y=ax2(a>0)上に2点A,Bがある。(1) OBとACの交点の座標をa,tを用いて表せ。 【解】B(t,at2)より,OBはy=atx これにx=-5を代入して, (-5,-5at) (2) △OABと△OACの面積の比が3:4のとき, ① tの値を求めよ。 【解】直線ABの切片は5at △OAB= △OAC= アイより, ② 4点O,A,B,Cが同一円周上にあるとき,aの値を求めよ。 【解】∠OBA=90°より,OA2=OB2+AB2 (-5)2+(25a)2=( |
||||||