 関数 |
１４ 放物線と直線１ | 月 日（ ） |
| 関数 |
１４ 放物線と直線１ | 月 日（ ） |
| １ | 法政大高校 （Ｒ４年） ★★ | ４ | 山梨県立高校 （Ｒ５年） ★ |
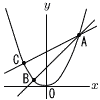 図のように放物線y＝ax2と,直線y＝x＋4は2点A,Bで,直線y＝ x＋6は2点A,Cで交わっている。(1) aの値を求めなさい。 (2) △ABCの面積を求めなさい。 |
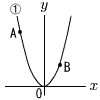 図において,①は関数y＝ax2(a＞0)のグラフであり,点A,Bは①上にある。点A,Bのx座標はそれぞれ－6,4である。(1) a＝  のとき,直線ABの式を求めなさい。(2) △AOBの面積が20になるときのaの値を求めなさい。 |
||
| ２ | 久留米大附設高校 （Ｒ５年） ★ | ５ | 近畿大附属高校 （Ｒ５年） ★★ |
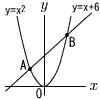 放物線y＝x2と直線y＝x＋6との交点をA,Bとする。Aのx座標は,Bのx座標より小さいものとする。(1) A,Bの座標をそれぞれ求めよ。 (2) y軸上に点Cをとる。3点A,B,Cが線分ABを直径とする円周上にあるとき,Cのy座標をすべて求めよ。 (3) 放物線y＝x2上に点Ｄ(t,t2)をとる。ただし,t＞０とする。また,直線y＝－3xと直線ADとの交点をEとする。 △OAE:△ODE＝1:3のとき,tの値を求めよ。 |
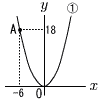 放物線y＝ax2…①がある。①は点A(－6,18)を通る。点Aを通り傾き１の直線と①の共有点でAでない方をB,点Bを通り傾き2の直線と①の共有点でBでない方をC,点Cを通り傾き－1の直線と①の共有点でCでない方をDとする。(1) aの値を求めよ。 (2) 直線ABの式を求めよ。 (3) 直線CDの式を求めよ。 (4) 面積比△ABD:△ACDを求めよ。 |
||
| ３ | 法政大第二高校 （R６年） ★★★ | ６ | 早稲田実業高等部 （R６年） ★★★ |
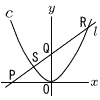 放物線C：y＝x2と直線l：y＝ax＋1がある。ただし,a＞0とする。lとx軸,y軸の交点をそれぞれ点Ｐ,Qとし,Cとlの交点のうち,x座標の大きい方の点をR,もう一方の点をＳとする。PQ＝QRのとき,(1) 点Ｒのy座標を求めなさい。 (2) aの値を求めなさい。 (3) RSの長さを求めなさい。 |
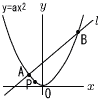 右の図のように,放物線y＝ax2(a＞0)上に2点A,Bがある。点Ａのx座標は－5,点Bのx座標はt(t＞0)である。また,点Ａからx軸に下ろした垂線の足をCとする。(1) 直線OBと直線ACの交点の座標をa,tを用いて表せ。 (2) △OABと△OACの面積の比が3:4のとき, ① tの値を求めよ。 ② 4点O,A,B,Cが同一円周上にあるとき,aの値を求めよ。 |
||
