 関数 |
１５ 放物線と直線２ （略解） | |
| 関数 |
１５ 放物線と直線２ （略解） | |
| １ | 中央大附属高校 （Ｒ５年） ★★ | ４ | 成城学園高校 （Ｒ５年） ★★ |
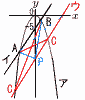 放物線y＝ax2…ア と直線y＝bx－5…イ は2点A,Bで交わる。(1) a,bの値を求めなさい。 【解】アイにA,Bのx座標を代入して (－5)2a＝－5b－5で,5a＋b＝－1…ウ 22a＝2b－5で，4a－2b＝－5…エ ウエを連立させて解くと, a＝－  , b＝ (2) 放物線上に点Cをとる。△ACBの面積が105となるとき,点Cの座標をすべて求めなさい。 【解】ABの平行線y＝  x＋p…ウをとる△ABP＝  (－5－p)×(2＋5)＝105より,p＝－35ウはy＝ x－35で,ア＝ウより,C(－10,－50) C(7,－49/2) |
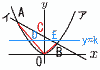 関数y＝ x2…ア と関数y＝ax＋b…イ が2点A,Bで交わっている。(1) a,bの値をそれぞれ求めよ。 【解】アより,A(－4,4) B(2,1) イにA(－4,4)を代入して,－4a＋b＝4…ウ イにB(2,1)を代入して,2a＋b＝1…エ ウエを連立させて解くと, a＝－ b＝2(2) △AOBの面積を求めよ。 【解】(1)より,C(0,2) △ＡＯＢ＝ OC×(BとAのx座標差)＝ ×2×(2＋4)＝6(3) kの値を求めよ。 【解】D(－k,k) E(4－2k,k)で,DE＝4－k △ACD＝ (4－k)2＝3で, k＝4－√6 |
||
| ２ | 桐朋高校 （Ｒ５年） ★★★ | ５ | 西大和学園高校 （Ｒ５年） ★★★ |
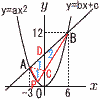 放物線y＝ax2…ア と直線y＝bx＋c…イ は2点A,Bで交わる。(1) a,b,cの値を求めよ， 【解】アにB(6,12)を代入して, a＝  イにA(－3,3) B(6,12)を代入して, b＝1,c＝6 (2) △APBの面積がy軸によって2等分されるとき, ① △ACBの面積は△APCの面積の何倍か。 【解】底辺CD共通で,△ACD:△BCD＝1:2  APCD＝△BCDより,△ACB:△APC＝3:1で, 3倍② 点Pの座標を求めよ， 【解】①より,BC:PC＝3:1で,Pのx座標は－2 y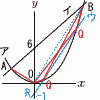＝  x2に代入して, P(－2, ) (3) 点Qのx座標を求めよ。 【解】△OAB＝27だから,△OQB＝3 OB  ウと引くと,△ORB＝3で,QBはy＝2x－1…ウ ア＝ウより, x2＝2x－1で, x＝3±√6 |
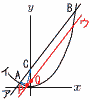 傾きが2である直線…ア が放物線y＝ax2…イ と2点A,Bで交わる。(1) 直線ABの式を求めよ。 【解】△OAC＝ OC×2＝6より, C(0,6)傾き2,y切片6となって, y＝2x＋6 …ア (2) aの値を求めよ。 【解】アにx＝－2を代入して,A(－2,2) これをイに代入して,2＝(－2)2aで, a＝ (3) 点Pの座標を求めよ。 【解】Pからアの平行線ウを引く △PAB＝△QABだから,QC:OC＝7:12で,Q(0, 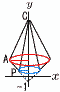 ) Pはイウの交点で,x2＝2x＋x2－4x－5＝0 x＜0より, P(－1, )(4) △CPAの回転体の体積を求めよ。 【解】 赤円錐(半径2,高さ4+3)－青円錐(半径  ,高さ)π×22×(4＋3)－π×１2×(＋)＝7π |
||
| ３ | 明学東村山高校 （R６年） ★★ | ６ | 関西学院高等部 （R６年） ★★★ |
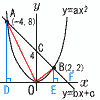 放物線y＝ax2…アと直線y＝bx＋c…イが2点A(－4,8),B(2,2)で交わっています。(1) a,b,cの値を求めなさい。 【解】アに(2,2)を代入して,2＝22aで, a＝ イに(－4,8)と(2,2)を代入して 連立させて解くと, b＝－1, c＝4 (2) 原点Oと2点A,Bを結んでできる△OABの面積 【解】△OAB＝ OC×(AとBのx座標差)△OAB＝ ×4×(2＋4)＝12(3) △OABをx軸に関して一回転させてできる立体の体積 【解】△FADの回転体－(△OADの回転体＋△BOFの回転体) ×82π×8－(×82π×4＋×22×4)＝80π |
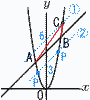 放物線y＝2x2…アと直線y＝x＋ …イの交点をA,Bとし,放物線上にある点をCとする。点Cのｘ座標はそのy座標の4倍であるとき。ただし,点Cは原点とは異なる点とする。(1) 点Cの座標を求めよ。 【解】C(k,4k)として,アに代入すると, 4k＝2k2より,k＝2で, C(2,8) (2) 点Pが放物線上を点Ａから点Ｂまで動くとき，△ACBと△APBの面積が等しくなるような点Ｐの座標を求めよ。 【解】ABの平行線①(切片6)と②(切片3)を引く ②はy＝x＋3…ウで,アウの交点がP 2x2＝x＋3より,x＝－1, で, P(－1,2) P(, ) |
||