| 侾俆丂曻暔慄偲捈慄俀 | 丂丂丂寧丂丂丂擔乮丂丂乯 |
| 侾俆丂曻暔慄偲捈慄俀 | 丂丂丂寧丂丂丂擔乮丂丂乯 |
| 侾 | 拞墰戝晬懏崅峑丂乮俼俆擭乯丂仛仛 | 係 | 惉忛妛墍崅峑丂乮俼俆擭乯丂仛仛 |
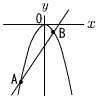 丂恾偺傛偆偵,曻暔慄y亖ax2偲捈慄y亖bx亅5偼2揰A,B偱岎傢傝,A,B偺x嵗昗偼偦傟偧傟亅5,2偱偁傞丅 丂恾偺傛偆偵,曻暔慄y亖ax2偲捈慄y亖bx亅5偼2揰A,B偱岎傢傝,A,B偺x嵗昗偼偦傟偧傟亅5,2偱偁傞丅(1) a,b偺抣傪媮傔側偝偄丅 (2) 曻暔慄忋偵揰C傪偲傞丅仮ACB偺柺愊偑105偲側傞偲偒,揰C偺嵗昗傪偡傋偰媮傔側偝偄丅 丂丂 |
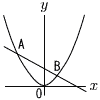 丂恾偺傛偆偵,娭悢y亖亅 丂恾偺傛偆偵,娭悢y亖亅(1) a,b偺抣傪偦傟偧傟媮傔傛丅 (2) 仮AOB偺柺愊傪媮傔傛丅 (3) 捈慄y亖k偑仮AOB偺柺愊傪2摍暘偡傞偲偒,k偺抣傪媮傔傛丅 丂 |
||
| 俀 | 嬎朁崅峑丂乮俼俆擭乯丂仛仛仛 | 俆 | 惣戝榓妛墍崅峑丂乮俼俆擭乯丂仛仛仛 |
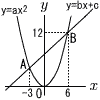 丂恾偺傛偆偵,曻暔慄y亖ax2偲捈慄y亖bx亄c偼2揰A,B偱岎傢傝,A偺x嵗昗偼亅3,B偺嵗昗偼(6,12)偱偁傞丅 丂恾偺傛偆偵,曻暔慄y亖ax2偲捈慄y亖bx亄c偼2揰A,B偱岎傢傝,A偺x嵗昗偼亅3,B偺嵗昗偼(6,12)偱偁傞丅(1) a,b,c偺抣傪媮傔傛丆 (2) 揰P傪y亖ax2忋偺亅3亙x亙0偺晹暘偵偲傝,慄暘PB偲y幉偺岎揰傪C偲偡傞丅仮APB偺柺愊偑y幉偵傛偭偰2摍暘偝傟傞偲偒, 丂嘆 仮ACB偺柺愊偼仮APC偺柺愊偺壗攞偐丅 丂嘇 揰P偺嵗昗傪媮傔傛丆 (3) 揰Q傪曻暔慄y亖ax2忋偺0亙x亙6偺晹暘偵偲傞丅巐妏宍OQBA偺柺愊偑30偲側傞偲偒,揰Q偺x嵗昗傪媮傔傛丅 丂丂 |
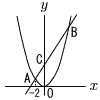 丂恾偺傛偆偵,孹偒偑2偱偁傞捈慄偑曻暔慄y亖ax2偲2揰A,B偱岎傢傝,y幉偲揰C偱岎傢偭偰偄傞丅尨揰傪侽偲偟,俙偺x嵗昗傪亅2,仮OAC偺柺愊傪6偲偡傞偲偒, 丂恾偺傛偆偵,孹偒偑2偱偁傞捈慄偑曻暔慄y亖ax2偲2揰A,B偱岎傢傝,y幉偲揰C偱岎傢偭偰偄傞丅尨揰傪侽偲偟,俙偺x嵗昗傪亅2,仮OAC偺柺愊傪6偲偡傞偲偒,(1) 捈慄AB偺幃傪媮傔傛丅 (2) a偺抣傪媮傔傛丅 (3) 揰P偼,曻暔慄y亖ax2忋偺揰A偲揰B偺娫偺揰偱,x嵗昗偑晧偱偁傞丅仮PAB偺柺愊偲仮OAB偺柺愊偺斾偑,仮PAB:仮OAB亖7:12偲側傞偲偒,揰P偺嵗昗傪媮傔傛丅 (4) (3)偺揰P偵懳偟偰,仮CPA傪y幉傑傢傝偵1夞揮偝偣偨偲偒偵偱偒傞棫懱偺懱愊傪媮傔傛丅 丂 |
||
| 俁 | 柧妛搶懞嶳崅峑丂乮R俇擭乯丂仛仛 | 俇 | 娭惣妛堾崅摍晹丂乮R俇擭乯丂仛仛仛 |
| 丂曻暔慄y亖ax2偲捈慄y亖bx亄c偑2揰A(亅4,8),B(2,2)偱岎傢偭偰偄傑偡丅 (1) a,b,c偺抣傪媮傔側偝偄丅 (2) 尨揰O偲2揰A,B傪寢傫偱偱偒傞仮OAB偺柺愊傪媮傔側偝偄丅 (3) 仮OAB傪x幉偵娭偟偰堦夞揮偝偣偰偱偒傞棫懱偺懱愊傪媮傔側偝偄丅 丂 |
 丂曻暔慄y亖2x2偲捈慄y亖x亄 丂曻暔慄y亖2x2偲捈慄y亖x亄(1) 揰C偺嵗昗傪媮傔傛丅 (2) 揰P偑曻暔慄忋傪揰俙偐傜揰俛傑偱摦偔偲偒,仮ACB偲仮APB偺柺愊偑摍偟偔側傞傛偆側揰俹偺嵗昗傪媮傔傛丅 丂 |
||