| 17 放物線と直線4 (略解) | ||
| 17 放物線と直線4 (略解) | ||
| 1 | 桜美林高校 (R4年) ★★ | 4 | 市立福山高校 (R5年) ★ | ||||||||||||
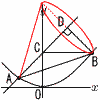 (1) aの値を求めなさい。 (1) aの値を求めなさい。【解】アに(-9,3)を代入して, 3=(-9)2aで, a=1/27 (2) 点Bの座標を求めなさい。 【解】ACの傾き=1だから,C(0,12) y= x=18で, B(18,12) (3) 1回転させてできる立体の体積 【解】D(9,21)で,BD=CD=9√2,AD=18√2 体積=外の円すい-内の円すい = |
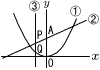 (1) t=-1のとき,線分PQの長さを求めなさい。 (1) t=-1のとき,線分PQの長さを求めなさい。【解】②,①にt=-1を代入して, P(-1, (2) PQ=2となるとき,tの値をすべて求めなさい。 【解】P(, PQ= t2-2t-9=0で, t=1±√10 (3) 平行四辺形になるとき,点Pの座標 【解】PQ=AOとなればよい PQ= |
||||||||||||||
| 2 | 京華高校 (R4年) ★★ | 5 | 立命館慶祥高校 (R5年) ★★★ | ||||||||||||
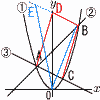 図のように,放物線y=ax2…①と2直線y=x+ 図のように,放物線y=ax2…①と2直線y=x+(1) aの値を求めよ。 【解】②=③より,A(-3, これを①に代入して, (2) 四角形ACBDが平行四辺形になるとき,点Dの座標を求めよ。 【解】①=②より,B(5, AD D(-3+3, (3) (2)のとき,直線DB上に△OBEの面積が90になるような点Eをとる。点Eの座標を求めよ。ただし,点Eのx座標は負とする。 【解】E(t,-t/2+15)とすると, △OBE= = 75-15t=180で,t=-7 よって, E(-7,37/2) |
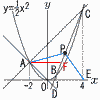 (1) 直線ACの式を求めなさい。 (1) 直線ACの式を求めなさい。【解】A(-2,2) C(4,8)
【解】B(1, OAはy=-x…ア BCはy= ア=イより,x= (3) △ADCの面積を求めなさい。 【解】F( △ADC= = (4) 点Pのx座標を求めなさい。 【解】P(t, △ADP= = △CEP=CE×(EとPのx座標差) = ウ=エより, t=260/119 |
||||||||||||||
| 3 | お茶の水女子大附属高校 (R6年) ★★ | 6 | 慶應義塾志木高校 (R6年) ★★★ | ||||||||||||
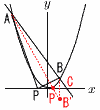 放物線①y=sx2(s<O)と2つの直線②y=tx,③y=-tx(t>0)において, 放物線①y=sx2(s<O)と2つの直線②y=tx,③y=-tx(t>0)において,(1) tの値を求めなさい。 【解】∠A=60°だから,傾きt=√3 (2) sの値を求めなさい。 【解】B(a,-√3a)とすると, △OAB= B(3,-3√3)で,これを①に代入して,-3√3a=32sで, s=- (3) さらに,放物線④y=px2(p<0)を考える。④と②,④と③の原点Oでない方の交点をそれぞれ点C,Dとおくとき,点C,Dの座標と△OCDの面積Sをpを用いて表しなさい。 【解】①=④より,√3x=px2で, C(√3/p,3/p) D(-√3/p,3/p)
|
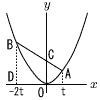 放物線y= 放物線y=(1) 直線lの方程式と点P,Qの座標を求めよ。 【解】(6,0),(0,6)を通るからlは, y=-x+6 …イ ア=イより, P(-1-√13,7+√13) Q((-1+√13,7-√13) (2) 直線l上に点B,Cをとって四角形OCABが長方形になるようにするとき,線分BCの長さを求めよ。 【解】BC=OAより, BC=√42+82=4√5 (3) (2)のとき,OCABの面積S1とOQAPの面積S2を求めよ。 【解】Aからl に垂線を下ろすと,H(1,5) AH=√(4-1)2+(8-5)2=3√2 S1=2△ABC=2×( lの傾きは-1なので,PQ=(QとPのx座標差)×√2=2√26 S2=2△APQ=2(( |
||||||||||||||