| 18 二つの放物線1 (略解) | ||
| 18 二つの放物線1 (略解) | ||
| 1 |
國學院久我山高校 (R4年) ★★ | 4 | 青雲高校 (R5年) ★★★ | |||||||||||||||||||||||||||||||||||
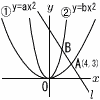 y=ax2…①,y=bx2…②と傾きが- y=ax2…①,y=bx2…②と傾きが-(1) aの値を求めなさい。 【解】①にA(4,3)を代入して, 42a=3より, a=3/16 (2) 直線l の式を求めなさい。 【解】y=- (3) 線分ABの長さを求めなさい。 【解】OA=5 △OAB= (4) bの値を求めなさい。 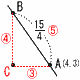 【解】(右図参照) 【解】(右図参照)AC: BC: ④⑤より, B(4- これを②に代入して,( |
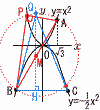 放物線y=x2上に点A,放物線y=- 放物線y=x2上に点A,放物線y=-(1) 点Cの座標を求めよ。 【解】C(c,- △OBCは正三角形だから,√3c= c( (2) △QBCの面積の最大値を求めよ。 【解】A(√3,3) B(-2√3,-6) PはABを直径とする円周上(半径3√3) 円の中心(ABの中点)はM(- 最大の△QBC= = |
|||||||||||||||||||||||||||||||||||||
| 2 | 岩手県立高校 (R6年) ★★ | 5 | 桐光学園高校 (R6年) ★★★ | |||||||||||||||||||||||||||||||||||
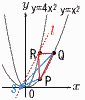 (1) 点Qの座標を求めなさい。 (1) 点Qの座標を求めなさい。【解】P(1,1)でR(1,4) アにy=4を代入して, Q(2,4) (2) aの値を求めなさい。 【解】P(a,a2),R(a,4a2),Q(2a,4a2)より,PR=3a2,QR=a 3a2=aで, a= (3) 点Sのx座標を求めなさい。 【解】(右上図参照) P(2,4),R(2,16)でQ(4,16) Rを通りPQ(傾き6)に平行な直線lを引き,x軸との交点をSとする 6(x-2)+16=0より, s=- |
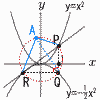 (1) 直線PRの式を求めよ。 (1) 直線PRの式を求めよ。【解】P(1,1),Q(1,-
【解】∠PQR=90°だから,PRは直径 (3)点Aのうち,y座標が最も大きいものの座標を求めよ。 【解】(右上図参照) PRに関してQの対称点をA(a,b)とする
|
|||||||||||||||||||||||||||||||||||||
| 3 | 桃山学院高校 (R6年) ★★ | 6 | 府立嵯峨野高校 (R6年) ★★ | |||||||||||||||||||||||||||||||||||
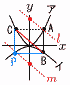 (1) aの値を水めなさい。 (1) aの値を水めなさい。【解】アに(2,8)を代入して, 8=22aより, a=2 (2) bの値[を求めなさい。 【解】B(2,4b),C(-2,8)で,AB=8-4b,AC=4 △ABC= (3) △ABCと△BCPの面積が等しくなるような点Pは,y=bx2のグラフ上に2つとれます。そのような点Pのx座標を求めなさい。 【解】(右上図参照) Aを通ってBCに平行なl は,y=- BCの下側に平行線mをとって,y=- Pはイとmの交点で,- x2-9x-22=0となって, x=-2,11 |
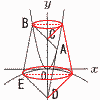 (1) 点Dの座標を求めよ。 (1) 点Dの座標を求めよ。【解】アより,A(2,4),B(-3,9)で, ABはy=-x+6 C(0,6)となるから, D(0,-6) (2) aの値を求めよ。 【解】DE これをイに代入して,-1=(-5)2aより, a=- (3) 四角彫BEDCを,y軸を回転の軸として1回転させてできる立体の体積を求めよ。 【解】(右上図参照) -上部凹円錐+円錐台+下部凸円錐 - =-9π+490/3π+125/3π=196π |
|||||||||||||||||||||||||||||||||||||