 関数 |
１８ 二つの放物線１ | 月 日（ ） |
| 関数 |
１８ 二つの放物線１ | 月 日（ ） |
| 1 | 國學院久我山高校 （Ｒ４年） ★★ | ４ | 青雲高校 （Ｒ５年） ★★★ |
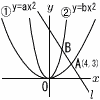 2つの放物線y＝ax2…①,y＝bx2…②と傾きが－ の直線l がある。直線l と放物線①,②の交点をそれぞれA,Bとする。直線OAと直線１が垂直に交わり,△OABの面積が ,A(4,3)であるとき,(3),(4)は途中過程も。(1) aの値を求めなさい。 (2) 直線l の式を求めなさい。 (3) 線分ABの長さを求めなさい。 (4) bの値を求めなさい。 |
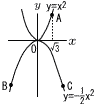 放物線y＝x2上に点A,放物線y＝－ x2上に2点B,Cをとる。原点をOとし,点Aのx座標は√3で,△OBCは正三角形である。ただし,点Cのx座標は正である。(1) 点Cの座標を求めよ。 (2) 放物線y＝－ x2上に点をとり,この点と点A,Bを結んだ三角形が直角三角形となるようにすると,この点は2つ存在する。このうち,x座標が小さい方をPとする。さらに,△ABPの外接円上に点Qをとる。△QBCの面積の最大値を求めよ。 |
||
| ２ | 岩手県立高校 （Ｒ６年） ★★ | ５ | 桐光学園高校 （Ｒ６年） ★★★ |
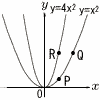 関数y＝x2のグラフ上に2点P,Qがあり,関数y＝4x2のグラフ上に点Ｒがあります。3点P,Q,Rのx座標は正であり,2点P,Rのx座標は等しく,2点Q,Rのy座標は等しいです。(1) 点Pのx座標を1とします。点Qの座標を求めなさい。 (2) 点Pのx座標をaとします。△PQRがPR＝QRの二等辺二角形になるとき,aの値を求めなさい。 (3) 点Pのx座標を2とします。x軸上にあり,x座標が負である点をSとします。△PQRと△PQSの面積が同じになるときの点Sのx座標を求めなさい。 |
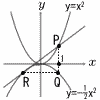 放物線y＝x2上にx座標が1である点Pをとる。また,放物線y＝－12x2上にx座標が1である点Q,点Qとy座標が等しい点Rをとる。△PQRの各頂点を通る円をCとするとき,(1) 直線PRの式を求めよ。 (2) 円Cの半径を求めよ。 (3) 円C上に△PQRの面積と△PARの面積が等しくなるように点Aをとる。このような点Aのうち,y座標が最も大きいものの座標を求めよ。 |
||
| ３ | 桃山学院高校 （Ｒ６年） ★★ | ６ | 府立嵯峨野高校 （Ｒ６年） ★★ |
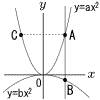 点A(2,8)は関数y＝ax2のグラフ上の点であり,点Aを通りx軸と垂直な直線と関数y＝bx2のグラフが交わる点をBとし,点Aとy軸について対称な点をCとします｡点Bのy座標が負であり,△ABCの面積が18であるとき,(1) aの値を求めなさい。 (2) bの値を求めなさい。 (3) △ABCと△BCPの面積が等しくなるような点Pは,y＝bx2のグラフ上に2つとれます｡そのような点Pのx座標を求めなさい。 |
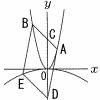 図のように,関数y＝x2がのグラフ上に2点Ａ,Ｂがあり,A,Bのx座標はそれぞれ2,－3である。直線ABとy軸との交点をCとしたとき,原点を中心として点Cと点対称な点をDとする。点Eが関数y＝ax2(a＜0)のグラフ上にあり,四角形ABEDが平行四辺形であるとき,(3)は答えを求める過程も(1) 点Ｄの座標を求めよ。 (2) aの値を求めよ。 (3) 四角彫BEDCを,y軸を回転の軸として１回転させてできる立体の体積を求めよ。 |
||
