１	玉川学園高校　（Ｒ５年）　★★	４	立命館守山高校　（Ｒ４年）　★★
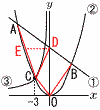y＝－x＋8…①　y＝x2…②　 　y＝(a＜0)…③ (1) aの値を求めよ。 【解】x＝－3を②に代入して,C(－3,3) Cを③に代入して,3＝a/(－3)で, a＝－9 (2) 点Bの座標を求めよ。 【解】－x＋8＝x2より,x2＋2x－24＝0で, B(4,) (3) 四角形ACOBの面積を求めよ。 【解】D(0,8) E(－14/3,8) 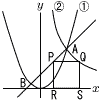ACOB＝△ACD＋OBDC ＝ED×(AとCのy座差)＋DO×(BとCのx座標差) ＝××9＋×8×7＝21＋28＝49		y＝ax2…①とxy＝54（x＞0）…② (1) aの値を求めなさい。 【解】②より,A(6,9)で,①に代入して, 　62a＝9より, a＝9/36＝ (2) 直線ABの式を求めなさい。 【解】①より,B(－2,1) y＝ 9－1 (x＋2)＋1で, y＝x＋3 6＋2 (3) 点Pの座標を求めなさい。 【解】P(t,t＋3)とすると, PQ＝PRより,Q(t＋t＋3,t＋3)＝Q(2t＋3,t＋3) これを②に代入して,(2t＋3)(t＋3)＝54 　2t2＋9t－45＝(2t＋15)(t－3)＝0で,t＝3　よって, P(3,6)
２	城北高校　（Ｒ５年）　★★	５	明大付属明治高校　（Ｒ４年）　★★★
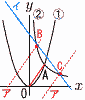2つの関数y＝x2…①,y＝（x＞0）…② (1) 点Aの座標を求めよ。 【解】x2＝より,x＝2で, A(2,2) (2) この2つの点の座標を求めよ。 【解】OA＝2√2だから,高さが OAから離れた平行線はy＝x±3 …ア 　＝x±3より,x2±3x－4＝0 　x＞0だから, (1,4)と(4,1) (3) 交点のx座標をすべて求めよ。 【解】BCはy＝－x＋5 …イ 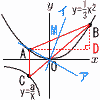x2＝－x＋5より,x2＋2x－10＝0で, x＝－1±√11		(1) t の値を求めよ。 【解】A(－t,t2) B(2t,t2) D(2t,t2) △ABDより,AD＝√3BD＝√3t2＝2t－(－t) 　√3t2＝3tより, t＝√3 (2) aの値を求めよ。 【解】C(－t,－a/√3) △ABC＝×(1＋a/√3)×3√3＝ 9√3 より, a＝2√3 2 (3) 原点Oを通り,△ABCを2:1に分ける直線の式 【解】 ア A(－√3,1)　OB:OC＝2:1　　直線OAで, y＝－√3x イ ABの中点M(√3,)　　直線OMで, y＝√3x
３	法政大国際高校　（Ｒ６年）　★★★	６	立命館高校　（Ｒ６年）　★★★
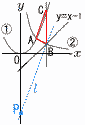放物線y＝ax2…①と曲線y＝(x＞0)…② (1) a,bの値を求めよ 【解】①に(1,1)を代入して,1=12aで, a＝1 ②に(1,1)を代入して,1＝b/1で, b＝1 (2) pの値を求めよ。 【解】Bのy座標＝p－1＝より, 　p＝ 1＋√5 2 (3) △ABCの面積を求めよ。 【解】B(p,p－1),C(p,p2)より, △ABC＝ ( 3＋√5 － √5－1 )( 1＋√5 －1)＝ √5－1 2 2 2 2 (4) Ｄのy座標のうち,最も小さいものを求めよ。 【解】Bを通ってACに平行な直線l を引く 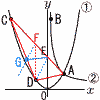ACの傾き＝( 3＋√5 －1)÷( 1＋√5 －1)＝ 3＋√5 2 2 2 l はBを通るから, √5－1 ＝ 3＋√5 × 1＋√5 ＋k(Pのy座標) 2 2 2 よって, k＝－ 5＋√5 2		(1) aの値を求めなさい。 【解】②上の点A(4,)を①に代入すると, ＝×42で, a＝16 (2) 直線ACの式を求めなさい。 【解】(1)より,A(4,4),B(1,16)で,C(－8,16) y＝ 4－16 (x－4)＋4で, y＝－x＋8 4＋8 (3) △ACDの面積を求めなさい。 【解】△ACDをFDで2分割 D(－2,1), AC上の点F(－2,10) △ＡＣＤ＝×(10－1)×(4＋8)＝54cm2 (4) 点Eを通り,△ACDの面積を2等分する直線の式 【解】△AFD＝△ACD＝27cm2 平行線を引いて,△FDE＝△MDEとなる点Gをとればよい FGは,y＝ 8－1 (x＋2)＋10＝x＋17…ア 0＋2 CDは,y＝ 1－16 (x＋2)＋1＝－x－4…イ －2＋8 アイより,G(－,)で, y＝x＋8

［TOP］　［問題にもどる］　　★　中　　★★　やや難　　★★★　難