 関数 |
２０ 放物線と双曲線 | 月 日（ ） |
| 関数 |
２０ 放物線と双曲線 | 月 日（ ） |
| １ | 玉川学園高校 （Ｒ５年） ★★ | ４ | 立命館守山高校 （Ｒ４年） ★★ |
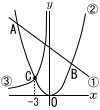 右の図の3つの関数について考える。y＝－  x＋8…① y＝ x2…② y＝  (a＜0)…③2点A,Bは①と②のグラフとの交点で,点Cは②と③のグラフとの交点であり,x座標は－3である。 (1) aの値を求めよ。 (2) 点Bの座標を求めよ。 (3) 四角形ACOBの面積を求めよ。 |
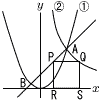 図において,点Aは放物線y＝ax2…①と双曲線xy＝54（x＞0）…②の交点で,点Bは①上にある。2点A,Bのx座標はそれぞれ6,－2である。(1) aの値を求めなさい。 (2) 直線ABの式を求めなさい。 (3) 線分AB上に点P,②上に点Qをとり,点Pを通りy軸に平行な直線とx軸との交点をR,点Qを通りy軸に平行な直線とx軸との交点をSとする。四角形PRSQが正方形のとき,点Pの座標を求めなさい。計算過程も解答欄に書きなさい。ただし,図を用いて説明してもよいものとする。 |
||
| ２ | 城北高校 （Ｒ５年） ★★ | ５ | 明大付属明治高校 （Ｒ４年） ★★★ |
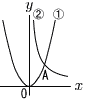 2つの関数y＝ x2…①,y＝ （x＞0）…②のグラフの交点をＡとする。(1) 点Aの座標を求めよ。 (2) ②のグラフ上の点Ｂで,△OABの面積が3となる点が2つある。この2つの点の座標を求めよ。 (3) (2)で求めた2点を通る直線と①のグラフの交点のx座標をすべて求めよ。 |
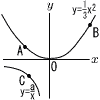 図のように,放物線y＝x2上に2点A,Bがあり,y＝（x＜0）のグラフ上に点Cがある。点A,Cのx座標はともに－t,点Bのx座標は2tである。∠BAC＝120°,△ABCの面積が √3であるとき(1) t の値を求めよ。 (2) aの値を求めよ。 (3) 原点Oを通り,△ABCの面積を2:1に分ける直線の式を求めよ。 |
||
| ３ | 法政大国際高校 （Ｒ６年） ★★★ | ６ | 立命館高校 （Ｒ６年） ★★★ |
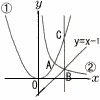 放物線y＝ax2…①と曲線y＝ (x＞0)…②が点Ａ(1,1)で交わっている。直線y＝x－1と曲線②との交点をBとし,Bのx座標をpとする。また,点Bを通りy軸に平行な直線と放物線①との交点をCとする。(1) a,bの値を求めよ (2) pの値を求めよ。 (3) △ABCの面積を求めよ。 (4) y軸上に点Dをとり,△ABCと△ADCの面積が等しくなるようにする。このような点Ｄのy座標のうち,最も小さいものを求めよ。 |
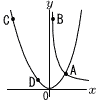 右の図のように,関数y＝ x2…①と関数y＝(a＞0,x＞0)…②のグラフがあります。点Aは①のグラフと②のグラフとの交点です。点Bは②のグラフ上にあり,2点A,Bのx座標はそれぞれ4,1です。点Cは①のグラフ上のx座標が負の部分にあり,点Bのy座標と点Cのy座標は等しくなっています。点Dは①のグラフ上にあり,x座標は－2です。ただし,座標軸の１目盛りを1cmとします,(1) aの値を求めなさい。 (2) 直線ACの式を求めなさい。 (3) △ＡＣＤの面積を求めなさい。 (4) 直線ACとy軸との交点をEとします。このとき,点Eを通り,△ACDの面積を2等分する直線の式を求めなさい。 |
||
