| �Q�P�@�������ƕ��s���@�i�����j | ||
| �Q�P�@�������ƕ��s���@�i�����j | ||
| �P | �����H�啍���ȋZ���Z�@�i�q�T�N�j�@���� | �S | �ˌ��w�����Z�@�i�q�T�N�j�@���� | ||||
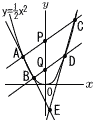 (1) �_A�̍��W�����߂Ȃ����B (1) �_A�̍��W�����߂Ȃ����B�y���zA(�|2k,2k2) C(3k,
(2) ����BD�̎������߂Ȃ����B �y���z(1)�Ɠ��l��,B(�|2,2) D(4,8)��, y��x�{4 (3) �y���zAC:BD��(6�{4):(4�{2)��5:3 ��EAC�䁢EBD(������5:3)���,��EAC:��EBD��25:9 �@S:T��(25�|9):9��16:9 |
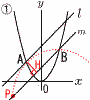 �@������y�� �@������y��(1) �_A�̍��W�����߂�B �y���z (2) ����m�̎������߂�B �y���zB(3, (3) �_A�Œ���l �ɐڂ���~��,����m���2�_B,P��ʂ�Ƃ�,�_P�̍��W�����߂�B �y���zAH��y���|(x�{2)�{2���|x��,H(�| H��PB�̒��_������, P(�| |
||||||
| �Q | ��@���Z�@�i�q�S�N�j�@������ | �T | ��@���Z�@�i�q�T�N�j�@���� | ||||
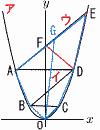 (1) D��E��x���W�@D�c[2t]�@E�c[3t] (1) D��E��x���W�@D�c[2t]�@E�c[3t]�y���zB(�|t,at2) C(t,at2) BD��,y��atx�{2at2�c�C ax2��atx�{2at2���,D(2t,4at2) A(�|2t,4at2) AE��,y��atx�{6at2�c�E ax2��atx�{6at2��� ,E(3t,9at2) (2) ��DEF�̖ʐς�a��t�ŕ\���B �y���zx���W���,AF:FE��2:3 ��DEF�� (3)a�̒l�����߂�B �y���zA��x���W�|2t���|3���,t�� �@�� �@��OGF��10at3�| ��OGF�� �@G��x���W��t��, �G���,G(t,7at2)��G( OG�̌X���� |
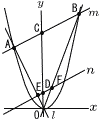 �@������y��ax2�c�@�ƒ���l:y���|2x������B �@������y��ax2�c�@�ƒ���l:y���|2x������B(1) A,B�̍��W��a��p���ĕ\����,A( , ) B( , )�ł���B �y���zax2���|2x���,x��0,�| m��y�� �@x���| (2) m��y���̌�_��C�Ƃ���B�_D(0,��)��ʂ蒼��m�ɕ��s�Ȓ�����n�Ƃ���Bl ��n�Ƃ̌�_��E�Ƃ�,n�ƒ���OB�Ƃ̌�_��F�Ƃ���B (a) ��ODF�̖ʐς�a��p���ĕ\���B �y���z ��ODF�� (b) ��ODF�̖ʐςƎl�pACDE�̖ʐς��������悤��a�̒l�����߂�B �y���z�|2x�� �@��OCA�� �@��ODE�� 5/a2�| |
||||||
| �R | �ߋE�啍�����Z�@�i�q�U�N�j�@������ | �U | ���u�Ѝ��Z�@�i�q�U�N�j�@������ | ||||
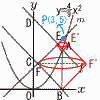 (1) a�̒l�����߂�B (1) a�̒l�����߂�B�y���zA���A�ɑ������,4�� (2) ����l �̎������߂�B �y���zB(3,0),C(03)���,BC�̌X���́|1 l ��y���|(x�|3)�{4��, y���|x�{7 (3) ����m�̎������߂�B �y���zm��
�y���z(��~��2��)�|(���~��2��)��, F( |
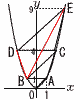 (1) ����BC�̕������Ɠ_E�̍��W�����߂�B (1) ����BC�̕������Ɠ_E�̍��W�����߂�B�y���zB(�|1,1),BC//OA���,BC��y��x�{2 x2��x�{2��,C(2,4),D(�|2,4) DE��y��x�{6��,x2��x�{6���, E(3,9) (2) ��ABC�Ɓ�CDE�̖ʐϔ���ł��ȒP�Ȑ����̔�ŕ\���B �y���z��ABC��3,��CDE��10���, �ʐϔ��3:10 (3) ��OAB�ƘZ�p�`OACEDB�̖ʐϔ� �y���z��OAB��1,�Z�p�`��1�{3�{6�{10��20���, 1:20 (4) �_E��ʂ�Z�p�`OACEDB������钼���̕����� �y���z��BDE����CDE��10���Z�p�`�~ EB��������, y��2x�{3 |
||||||