| �Q�R�@�������ƎO�p�`�@�i�����j | ||
| �Q�R�@�������ƎO�p�`�@�i�����j | ||
| �P | ���{�@��v��R���Z�@�i�q�T�N�j�@���� | �S | ����c���ƍ������@�i�q�S�N�j�@������ | |||||||||||||||||||||||||
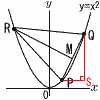 �@�}�̂悤��,������y��x2���3�_P,�p,R������BP,�p,R��x���W�����ꂼ��p,q,r�ir��p��q�j�Ƃ���B��PQR��RP��RQ,PQ����5�̓Ӄ��p�`�ł���,����PQ�̌X����2�ł���B�܂�,PQ�̒��_��M�Ƃ����,����MR�̌X���́| �@�}�̂悤��,������y��x2���3�_P,�p,R������BP,�p,R��x���W�����ꂼ��p,q,r�ir��p��q�j�Ƃ���B��PQR��RP��RQ,PQ����5�̓Ӄ��p�`�ł���,����PQ�̌X����2�ł���B�܂�,PQ�̒��_��M�Ƃ����,����MR�̌X���́|(1) q�|p�̒l�����߂Ȃ����B �y���z��PQS��,PQ����5, QS/PS�� PS��q�|p��1�c�A (2) q�̒l�����߂Ȃ����B �y���zQS��q2�|p2��2 �c�C �A���,p��q�|1��,������C�ɑ������, �@q2�|(q�|1)2��2��, q�� (3) r�̒l�����߂Ȃ����B(�r���ߒ����L��) �y���zP(
|
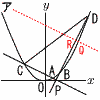 (1) �_D�̍��W��,����CD�̎� (1) �_D�̍��W��,����CD�̎��y���z PA��,y���| PB��y��2x�|3 �@ �C�E���, CD��y�� (2) ��PAB:��PCD�����߂�B �y���z PA:PC��( AB�aCD���,��PAB:��PCD=12:92��1:81 (3) Q�̍��W�����߂�B �y���zPD���R���Ƃ�,RQ//CP�Ƃ��� ��ABDC��2��QAC��2RAC��2S�Ƃ��� �@��RPC����DPC�~
|
|||||||||||||||||||||||||||
| �Q | �O�d�������Z�@�i�q�S�N�j�@���� | �T | �R�w�@�������@�i�q�S�N�j�@���� | |||||||||||||||||||||||||
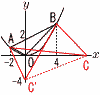 (1) �_A,B��ʂ钼���̎� (1) �_A,B��ʂ钼���̎��y���zA�|2,1)�@B(4,4)
�y���zC'(0,�|4)����AB�aC'C��������, �@��C'AB����CAB��,��OAB:��CAB��1:3 C'C��y�� �A �_D�̍��W�����߂Ȃ����B �y���z(AD�̌X��)�~(BD�̌X��)���|1
|
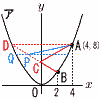 (1) a�̒l�����߂�D (1) a�̒l�����߂�D�y���z�A��(4,8)��������, 42a��8���, a�� (2) ����BC�̎������߂�D �y���zy���Ώ̓_D(�|4,8)�@B(2,2) ����BC������BD��, y���|x�{4 �c�C (3) �_P�̍��W�����߂�B �y���zBC��PD�ƂȂ�P���Ƃ��,P��x���W�́|2 �C��x���|2��������, P(�|2,6) (4) �_Q�̍��W�����߂�B �y���z��ADQ����ADP�ƂȂ�Q���Ƃ� DA�aQP���, |
|||||||||||||||||||||||||||
| �R | �x��b�{���Z�@�i�q�U�N�j�@���� | �U | �c��`�m���Z�@�i�q�U�N�j�@������ | |||||||||||||||||||||||||
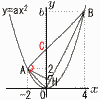 (1) a,b�̒l�����ꂼ�ꋁ�߂�B (1) a,b�̒l�����ꂼ�ꋁ�߂�B�y���z�A�ɂ`��������,2��(�|2)2a��, a�� y�� (2) �O�p�`OAB�̖ʐς����߂�B �y���zAB��y��x�{4��,C(0,4) ��OAB�� �@�@�� (3) �O�p�`OAH�̖ʐς����߂�B �y���zOB��4��5,OA��2��2 ��OAB�䁢OHA��,�ʐϔ��(4��5)2�F(2��2)2��10:1 �����,��OAH�� |
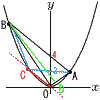 (1) �_B�̍��W�����߂�B (1) �_B�̍��W�����߂�B�y���zOA�̌X���� (2) �_C�̍��W�����߂�B �y���zAB�ɕ��s��y���| (3) ����OD�̒��������߂�B �y���z��OAB�� ��BOC����AOC�� �A�{�C���,OABC��32������,��ABD��16�ɂȂ�悢�B �A���,OD�� |
|||||||||||||||||||||||||||