 関数 |
２３ 放物線と三角形 | 月 日（ ） |
| 関数 |
２３ 放物線と三角形 | 月 日（ ） |
| １ | 國學院大久我山高校 （Ｒ５年） ★★ | ４ | 早稲田実業高等部 （Ｒ４年） ★★★ |
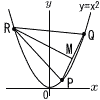 図のように,放物線y＝x2上に3点P,Ｑ,Rがある。P,Ｑ,Rのx座標をそれぞれp,q,r（r＜p＜q）とする。△PQRはRP＝RQ,PQ＝√5の二等辺Ξ角形であり,直線PQの傾きは2である。また,PQの中点をMとすると,直線MRの傾きは－ である。(1) q－pの値を求めなさい。 (2) qの値を求めなさい。 (3) rの値を求めなさい。(途中過程も記す) |
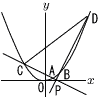 放物線y＝ x2…ア上に2点A,Bがあり,そのx座標はそれぞれ1,2である。x軸上に点P( ,0)をとり,直線PAとアとの交点で点Aと異なるものを点C,直線PBとアとの交点で点Bと異なるものを点Dとするとき,(1) 点Dの座標と,直線CDの式を求めよ。 (2) △PAB:△PCDを求めよ。 (3) 放物線上に点Qをとる。△QACの面積が四角形ABCDの面積の になるとき,Qの座標を求めよ。ただし,Qのx座標は正とする。 |
||
| ２ | 三重県立高校 （Ｒ４年） ★★ | ５ | 青山学院高等部 （Ｒ４年） ★★ |
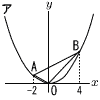 図のように,関数y＝x2…ア のグラフ上に2点A,Bがあり,点Ａのx座標が－2,点Ｂのx座標が4である。3点O,A,Bを結び△OABをつくる。(1) 点A,Bを通る直線の式を求めなさい。 (2) x軸上のx＞０の範囲に2点C,Dをとり,△ABCと△ABDをつくる。 ① △OABの面積と△ABCの面積の比が1:3となるとき,点Cの座標を求めなさい。 ② △ABDが∠ADB＝90°の直角三角形となるとき,点Dの座標を求めなさい。 |
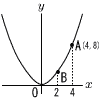 関数 y＝ax2…ア のグラフ上に2点A,Bがあり,Aの座標は(4,8),Bのx座標は2である。また,y軸上にAC＋BCが最も小さくなるような点Cをとる。(1) aの値を求めよ． (2) 直線BCの式を求めよ． ここで,直線BCとアのグラフの交点で,Bでない方をDとする。 (3) 線分BD上に,△ADPと△ABCの面積が等しくなるような点Pをとる。点Pの座標を求めよ。 (4) アのグラフ上に,△ADQと△ABCの面積が等しくなるような点Qをとる。ただし,点Qは2点B,Dの間にある。点Qの座標を求めよ。 |
||
| ３ | 駿台甲府高校 （Ｒ６年） ★★★ | ６ | 慶應義塾高校 （Ｒ６年） ★★★ |
 右図のように,関数y＝ax2のグラフ上に2点Ａ(－2,2),B(4,b)がある。(1) a,bの値をそれぞれ求めよ。 (2) 三角形OABの面積を求めよ。 (3) 点Ａから線分OBに垂線ＡＨをひくとき,三角形OAHの面積を求めよ。 |
 放物線y＝x2上に点Ａ(2,1)と∠AOB＝90゜となる点Bの2点がある。(1) 点Bの座標を求めよ。 (2) 放物線y＝ x2上で,かつ直線OBの下側にあり,△ABCの面積と△OABの面積を等しくするような点Cの座標を求めよ。(3) (2)の点Cについて,点Bを通り四角形OABCの面積を二等分する直線と,直線OAとの交点をDとするとき,線分ODの長さを求めよ。 |
||
