 関 数 |
２４ 放物線と四角形１ （略解） | |
| 関 数 |
２４ 放物線と四角形１ （略解） | |
| １ | 愛知県立高校Ｂ （Ｒ４年） ★ | ５ | 渋谷教育学園幕張高校 （Ｒ４年） ★★★ | ||||||||||||||||
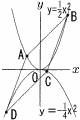 図で,0は原点,A,Bは関数y＝ x2のグラフ上の点で,x座標はそれぞれ－2,4である。また,C,Dは関数y＝－ x2のグラフ上の点で,点Cのx座標は点Dのx座標より大きい。四角形ADCBが平行四辺形のとき,点Dのx座標を求めなさい。【解】AとBのx座標差は6 D(k,－ k2)とすると, C(k＋6,－k2＋6)Cはy＝－ x2上にあるから,－ k2＋6＝－(k＋6)2k2－24＝k2＋12k＋36で, k＝－5 |
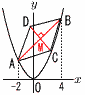 (1) 直線CDの式を求めなさい。【解】ひし形は,対角線が中点で直交
(2) 点Dの座標を求めなさい。 【解】Cのx座標c,Dのx座標dを求める x2＝－x＋6より,c＝－1＋√13
|
||||||||||||||||||
| ２ | 愛光高校 （Ｒ５年） ★★★ | ６ | 東大寺学園高校 （Ｒ４年） ★★★ | ||||||||||||||||
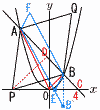 右の図のように,放物線y＝x2と直線y＝－x＋4が2点A,Bで交わっている。また,x軸上に点Pをとり,さらに四角形APBQが平行四辺形となるように点Qをとる。ただし,点Pのx座標は4より小さいとする。(1) 点A,Bの座標を求めよ。答のみでよい。 【解】 x2＝－x＋4より,x＝－4,2A(－4,8) B(2,2) (2) 点P,Qの座標を求めよ。 【解】△APB＝  △AOBになればよいDP:BO＝CP:CO＝3:2より, P(－2,0) D(－1,5)は対角線の交点だから, Q(0,10) (3) 点Pの座標を求めよ。 【解】B'(2,－2)をとると,AB'はy＝－  x＋  …ア点は右上図のEで,アにy＝0を代入して, P(  ,0) |
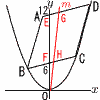 図のように原点をOとするxy平面上に点A(－2,11)と放物線y＝x2上の3点B,C,Dがあり,四角形ABCDは平行四辺形である。(1) Cのx座標を求めよ。 【解】B(－4,4) C(c, c2)とすると,y座標より,(c＋2)2－c2＝11－4で, c＝6 (2) l の式を求めよ。 【解】l は,対角線の交点Mを通る ACの中点で,M(2,10)より, y＝5x (3) mの式を求めよ。 【解】△OEG∽△OFH(相似比は2:1) H,Gのx座標をk,2kとすると, S:(S＋T)＝(AG＋BH):2BC＝2:5で, x座標より,(2k＋2＋k＋4):20＝2:5 k＝  , H(, )となって, y＝ x |
||||||||||||||||||
| ３ | 日本大第二高校 （Ｒ６年） ★ | ７ | 桜美林高校 （Ｒ６年） ★★ | ||||||||||||||||
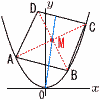 原点を通り,平行四辺形ABCDの面積を二等分する直線の方程式を求めよ。【解】対角線ACの中点Mを求める A(－6,18),C(8,32)より,M（1,25) 二等分線はOMで, y＝25x |
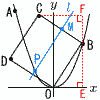 放物線y＝ax2(a＞0)…ア(1) aの値を求めなさい。 【解】アにA(－8,16)を代入して, 16＝(－8)2aで, a＝16/64＝  (2) 点Bの座標を求めなさい。 【解】B(b, b2)とすると,CF＝BEより,b－(－3)＝b2これを解いてb＝6で, B(6,9) (3) 放物線y＝ax2のx座標が負である部分に点Pをとる。BP＝CPとなるとき,点Pのx座標を求めなさい。 【解】BCの垂直二等分線l との交点がP FE＝6＋9＝15より,C(－3,15)で,M( ,12)l はy＝ (x－)＋12＝x＋ …イア＝イより, x2＝x＋で, x＝3－4√3 |
||||||||||||||||||
| ４ | 成蹊高校 （Ｒ６年） ★ | ||||||||||||||||||
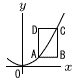 関数y＝ x2…ア(1) 点Cの座標を求めよ。 【解】A(1, ) 1辺をtとすると,C(1＋t,＋t)アにCを代入して, ＋t＝(1＋t)2より,t＝1で, C(2,  )⑵ ∠ADB＝30°でAD＝3のとき,点Aの座標を求めよ。 【解】A(a, a2)とすると,C(a＋√3,a2＋3)アにCを代入して, a2＋3＝(a＋√3)2より,a＝√3で, A(√3,1) |
|||||||||||||||||||