| 24 放物線と四角形1 | 月 日( ) |
| 24 放物線と四角形1 | 月 日( ) |
| 1 | 愛知県立高校B (R4年) ★ | 5 | 渋谷教育学園幕張高校 (R4年) ★★★ |
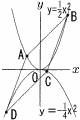 図で,0は原点,A,Bは関数y= 図で,0は原点,A,Bは関数y= |
放物線y= (1) 直線CDの式を求めなさい。 (2) 点Dの座標を求めなさい。 |
||
| 2 | 愛光高校 (R5年) ★★★ | 6 | 東大寺学園高校 (R4年) ★★★ |
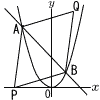 右の図のように,放物線y= 右の図のように,放物線y=(1) 点A,Bの座標を求めよ。答のみでよい。 (2) 平行四辺形APBQの面積が,△AOBの面積の3倍となるような点P,Qの座標を求めよ。 (3) 平行四辺形APBQの周の長さが最も短くなるような点Pの座標を求めよ。 |
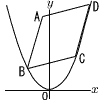 図のように原点をOとするxy平面上に点A(-2,11)と放物線y= 図のように原点をOとするxy平面上に点A(-2,11)と放物線y=(1) Cのx座標を求めよ。 (2) Oを通る直線l によって平行四辺形ABCDの面積が二等分されるとき,l の式を求めよ。 (3) Oを通る直線mで平行四辺形ABCDを2つの部分に分け,Bを含むほうの図形の面積をS,Bを含まないほうの図形の面積をTとする。S:T=2:3となるようなmの式を求めよ。 |
||
| 3 | 日本大第二高校 (R6年) ★ | 7 | 桜美林高校 (R6年) ★★ |
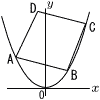 図のように,放物線y= 図のように,放物線y= |
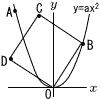 図のように,放物線y=ax2(a>0)上に点A,Bがあり,点Aの座標は(-8,16),点Bのx座標は正の数である。また,点Oは原点,四角形BODC は正方形で,点Cのx座標は-3である。 図のように,放物線y=ax2(a>0)上に点A,Bがあり,点Aの座標は(-8,16),点Bのx座標は正の数である。また,点Oは原点,四角形BODC は正方形で,点Cのx座標は-3である。(1) aの値を求めなさい。 (2) 点Bの座標を求めなさい。 (3) 放物線y=ax2のx座標が負である部分に点Pをとる。BP=CPとなるとき,点Pのx座標を求めなさい。 |
||
| 4 | 成蹊高校 (R6年) ★ | ||
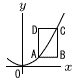 図のように,関数y= 図のように,関数y=(1) 点Aのx座標が1で四角形ABCD が正方形であるとき,点Cの座標を求め よ。 (2) ∠ADB=30°でAD=3のとき,点Aの座標を求めよ。 |
|||