関数 ２６　座標平面１　（略解）
１ 愛知県立高校A　（Ｒ４年）　★★ ５ 千葉県立高校　（Ｒ５年）　★★
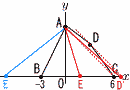　図で,Oは原点.点A,B,C,Dの座標はそれぞれ(0,6),(－3,0),(6,0),(3,4)である。また,Eはx軸上を動く点である。
　△ABEの面積が四角形ABCDの面積の倍となる場合が2通りある。このときの点Eの座標を2つとも求めなさい。

【解】DからACの平行線を引く
ACの傾きは－1で,DD'はy＝－(x－3)＋4＝－x＋7
Eは,D'(7,0)とBの中点で, E(2,0)
もう1つは,Bとの対称点で, E(－8,0)		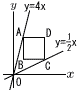 　図のように,直線y＝4x…ア 上の点Aと直線y＝x…イ 上の点Cを頂点にもつ正方形ABCDがある。点Aと点Cのx座標は正で,辺ABがy軸と平行であるとき,

(1)点Aのy座標が8であるとき,
① 点Aのx座標を求めなさい。
【解】アにy＝8を代入して,8＝4xより, x＝2

② 2点A,Cを通る直線の式を求めなさい。
【解】A(2,8)を通って,傾き－1の直線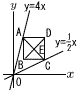
y＝－(x－2)＋8より, y＝－x＋10

(2)正方形ABCDの対角線ACと対角線BDの交点をEとする。点Eのx座標が13であるとき,点Dの座標を求めなさい。
【解】D(p,q)とすると,C(p,p)
ACはy＝－x＋pで,4x＝－x＋pより,A(p,p)
EはACの中点だから,(p＋p)＝13で,p＝20
D(p,p)＝D(20,24)
２ 城北高校　（Ｒ５年）　★★
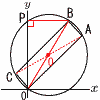　座標平面上にある長方形OABCの外接円とy軸との交点Ｐの座標を求めよ。ただし,O(0,0),A(4,4),C(－1,1)とする。

【解】OBは直径で,∠OPB＝90°
OACBより,B(3,5)で, P(0,5)
　
３ 早大本庄高校　（Ｒ４年）　★★★ ６ 駿台甲府高校　（Ｒ５年）　★★★
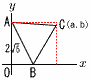　座標平面上に,2点A(0,4),B(2,0)がある。点C(a,b)を三角形 ABCが正三角形になるようにとるとき,定数a,bの値をそれぞれ求めよ。

【解】
AC2=BC2より,a2＋(4－b)2＝(a－2)2＋b2
　これを解いて, a＝2b－3…ア
また,AC2=(2√5)2＝20とアより,
　(2b－3)2＋(4－b)2＝20
　b2－4b＋1＝0で,b＝2±√3
b＝2＋√3のとき,　a＝2(2＋√3)－3＝1＋2√3
b＝2－√3のとき,
　a＝2(2－√3)－3＝1－2√3＜0 (不適)		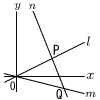 　直線l の式はy＝x,直線mの式はy＝－xである。直線l 上にx座標が正である点Pがあり,点Pを通り,傾きが－である直線をn,2直線m,nの交点をQとする。
　線分PQ上にある格子点の個数が7個であるとき,点Qの座標を求めよ。

【解】Q(4t,－t)とすると,
Pは左上(傾き－)へ6個目の格子点
　Pのx座標は,4t－2×6＝4t－12
　Pのy座標は,－t＋5×6＝－t＋30
Pの座標をl に代入して,－t＋30＝(4t－12)
　t＝12となって, Q(48,－12)
　
４ 早稲田実業高等部　（Ｒ６年）　★ ７ ラ・サール高校　（Ｒ６年）　★
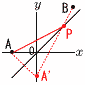　座標平面上に２点Ａ(－3,0),B(4,5)があり,直線y＝x上に点Pをとる。AP＋BPが最小となるような点Pの座標を求めよ。答えに至るまでの過程も丁寧に記述すること。

【解】y＝xに関してAの対称点A'(0,－3)をとる
このとき,AP＋BP＝A'P＋BPとなるから,
　A'Bが一直線y＝2x－3のとき最短となる
x＝2x－3より,x＝3で, P(3,3)		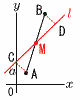 　座標平面上に2点Ａ(1,1),Ｂ(3,6)と直線l：y＝x＋aがある。A,Bからl に垂線を引き,l との交点をそれぞれC,Dとすると,AC＝BDとなった。
　このとき,定数aの値を求めよ。

【解】△ACM≡△BDM
CDの中点M(2,）を通ればよい
＝2＋aより, a＝
　

［TOP］　［問題に戻る］　★　中　　★★　やや難　　★★★　難