| 27 座標平面2 (解答) | ||
| 27 座標平面2 (解答) | ||
| 1 | 徳島県立高校 (R6年) ★ | 5 | 鹿児島県立高校 (R4年) ★★ | |||||||||
【解】傾きの符号逆,切片は同じ y=3x+1 |
直線y=-x+2a…① (1) ①がAB と交わるときのaの範囲 【解】 ①がAを通るとき,-2+2a=4より,a=3 ①がBを通るとき,-8+2a=4より,a=6 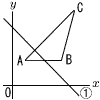 よって, 3≦a≦6 よって, 3≦a≦6(2) 点Qの座標をaを用いて表せ。 【解】
よって, Q(a-1,a+1) (3) △APQ= 【解】△ABC= △APQ= (a-3)2=3で,3≦a≦6より, a=3+√3 |
|||||||||||
| 2 | 桜美林高校 (R5年) ★ | |||||||||||
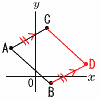 a,bをともに正の数とする。座標平面上に4点A(-5,6) ,B(3,-1),C(2,10),D(a,,b)がある。この4点を頂点とする四角形が平行四辺形になるとき,a,bの値を求めなさい。 a,bをともに正の数とする。座標平面上に4点A(-5,6) ,B(3,-1),C(2,10),D(a,,b)がある。この4点を頂点とする四角形が平行四辺形になるとき,a,bの値を求めなさい。【解】AC A→Cは, x座標が+7, y座標が+4 B→Dは, a=3+7=10 b=-1+4=3 |
||||||||||||
| 3 | 明治大付属八王子高校 (R5年) ★★ | 6 | 東京工大附属科技高校 (R4年) ★★★ | |||||||||
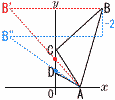 右の図において,点Aと点Bの座標はそれぞれ(2,0)と(4,7)であり,2点C,Dはy軸上の点です。 右の図において,点Aと点Bの座標はそれぞれ(2,0)と(4,7)であり,2点C,Dはy軸上の点です。(1) 三角形ABCの周の長さがもっとも短くなるとき,点Cの座標を求めなさい。 【解】B'(-4,7)をとると,Cは図の赤点 AB'は,y=- (2) 点Cのy座標は点Dのy座標より2だけ大きいです。四角形ABCDの周の長さがもっとも短くなるとき,点Cの座標を求めなさい。 【解】B''(-4,5)をとると,Dは図の青点 AB''は,y=- |
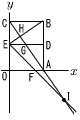 (1) 点Hの座標を求めなさい。 (1) 点Hの座標を求めなさい。【解】 ACはy=- BEはy= ア=イより,- x= (2) 点I の座標を求めなさい。 【解】EF=ED=5より,F(3,0) EFはy=- ア=ウより,- x=15で, I (15,-16) (3) ,S:Tを簡単な整数の比で表しなさい。 【解】△EHG=Uとすると,G( U:S=HG:HI=(
|
|||||||||||
| 4 | 西大和学園高校 (R6年) ★★ | 7 | 慶應義塾志木高校 (R6年) ★★ | |||||||||
| 直線4x+5y=2…ア,ax+3y=…イ0の交点をPとし,直線-x+2y=7…ウ,5x+by=-1…エの交点をQとすると,P,Qは原点に関して対称になった。このとき,a,bの値を求めよ。 【解】P(m,n),Q(-m,-n)とする
エにQ(-3,2)を代入すると,5×(-3)+2b=-1で, b=7 |
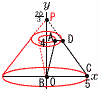 4点A(1,6),B(0,2),C(5,2),D(2,6)を頂点とする四角形ABCDをy軸を軸として1回転してできる立体の体積Vを求めよ。 4点A(1,6),B(0,2),C(5,2),D(2,6)を頂点とする四角形ABCDをy軸を軸として1回転してできる立体の体積Vを求めよ。【解】y軸方向に-2移動して考える 直線CDの切片はP(0, V=大円錐-上部凸小円錐-下部凹小円錐 = |
|||||||||||