関数

２７　座標平面２

月　　　日（　　）

１	徳島県立高校　（Ｒ６年）　★	５	鹿児島県立高校　（Ｒ４年）　★★
y軸を対称の軸として,直線y＝−3x＋1と線対称となる直線の式を求めなさい。		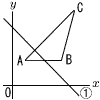図は,直線y＝−x＋2a…�@と△ABCを示したものであり,3点A,B,Cの座標は,それぞれ(2,4),(8,4),(10,12)である。 　直線�@が線分ABと交わるとき,直線�@と線分AB.,ACの交点をそれぞれP,Qとする。ただし,点Aと点Bのどちらか一方が直線�@上にある場合も,直線�@と線分ABが交わっているものとする。 (1) 直線�@が線分AB と交わるときのaの値の範囲を求めよ。 (2) 点Qの座標をaを用いて表せ。 (3) △APQの面積が△ABCの面積のであるとき,aの値を求めよ。ただし,求め方や計算過程も書くこと。
２	桜美林高校　（Ｒ５年）　★
a,bをともに正の数とする。座標平面上に4点A(−5,6) ,B(3,−1),C(2,10),D(a,,b)がある。この4点を頂点とする四角形が平行四辺形になるとき,a,bの値を求めなさい。
３	明治大付属八王子高校　（Ｒ５年）　★★	６	東京工大附属科技高校　（Ｒ４年）　★★★
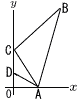右の図において,点Aと点Bの座標はそれぞれ(2,0)と(4,7)であり,2点C,Dはy軸上の点です。 (1) 三角形ABCの周の長さがもっとも短くなるとき,点Cの座標を求めなさい。 (2) 点Cのy座標は点Dのy座標より2だけ大きいです。四角形ABCDの周の長さがもっとも短くなるとき,点Cの座標を求めなさい。		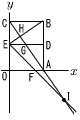図のように長方形ABCOがある。2点A,Cはそれぞれx軸上,y軸上にあり,点Bの座標は(5,8)である。辺AB,COの中点をそれぞれD,E,線分EDをEを中心として時計回りに回転させたとき,点Dがx軸に到達した点をＦとする。また,対角線ACと線分DE,BEとの交点をG,H,直線ACとEFの交点をI とする。 (1) 点Hの座標を求めなさい。 (2) 点Ｉの座標を求めなさい。 (3) △EHI の面積をS,四角形BDGHの面積をTとするとき,S:Tをもっとも簡単な整数の比で表しなさい。
４	西大和学園高校　（Ｒ６年）　★★	７	慶應義塾志木高校　（Ｒ６年）　★★
直線4x＋5y＝2,ax＋3y＝0の交点をPとし,直線−x＋2y＝7,5x＋by＝−1の交点をQとすると,P,Qは原点に関して対称になった。このとき,a,bの値を求めよ。		4点A(1,6),B(0,2),C(5,2),D(2,6)を頂点とする四角形ABCDをy軸を軸として1回転してできる立体の体積Vを求めよ。

［TOP］［BACK］［NEXT］［解答］　　★中 ★★やや難 ★★★難　 印刷用