| 29 動点1 (略解) | ||
| 29 動点1 (略解) | ||
| 1 | 帝京高校 (R4年) ★★ | 4 | 鹿屋中央高校 (R4年) ★★ |
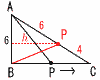 図のようなAB=6cm,BC=8cm,CA=10cmの直角三角形ABCにおいて,点Pは辺BC,CA上を点BからCを通り,Aまで毎秒2cmの速さで動く。点Pが点Bを出発してからx秒後の三角形ABPの面積をycm2とするとき, 図のようなAB=6cm,BC=8cm,CA=10cmの直角三角形ABCにおいて,点Pは辺BC,CA上を点BからCを通り,Aまで毎秒2cmの速さで動く。点Pが点Bを出発してからx秒後の三角形ABPの面積をycm2とするとき,(1) 0<x<4のとき,yをxの式で表しなさい。 【解】PはBC上で,BP=2x y= (2) x=6のとき,yの値を求めなさい。 【解】PはCA上で,CP=4 h:8=6:10より,h= y= |
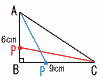 (1) 点Pが頂点Aを出発してから4秒後のとき,△APCの面積を求めよ。 (1) 点Pが頂点Aを出発してから4秒後のとき,△APCの面積を求めよ。【解】PはAB上で,AP=4 △APC= (2) △APCの面積が12cm2となるのは,点Pが頂点Aを出発してから何秒後か,すべて求めよ。 【解】x秒後とすると, ・PがAB上(0≦x≦6)のとき, △APC= ・PがBC上(6≦x≦15)のとき, △APC=△ABC-△ABP = |
||
| 2 | 早稲田佐賀高校 (R4年) ★★★ | 5 | 就実高校 (R5年) ★★ |
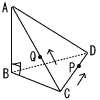 図のように,三角すいABCDがある。 図のように,三角すいABCDがある。(1) 三角すいABCDの体積V0を求めよ。 【解】 V0= (2) 1秒後の三角すいBCPQの体積V1 【解】底面はV0の V1= つまりV0の (3) ,三角すいBCPQの体積がV1と等 しくなったとき,tの値 【解】PがDB上(3≦t≦6)のとき,PB=6-t 底面はV0の V1= (6-t)t=1で, t=3+2√2 |
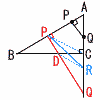 AB=10cm,BC=8cm,CA=6cmの直角三角形がある。 AB=10cm,BC=8cm,CA=6cmの直角三角形がある。(1) 3秒後のとき,APの長さとAQの長さを求めなさい。 【解】△AQP∽△ABC(比は3:4:5) AP=3cm AQ=5cm (2) 6秒後のとき,四角形APDCの面積を求めなさい。 【解】AQ=10より,CQ=4,CD=3 APDC=△APQ-△DCQ=24-6=18cm2 (3) (2)のとき,線分AQ上に点Rを△APRと四角形APDCの面積が等しくなるようにとる。線分ARの長さを求めなさい。 【解】DからPCの平行線を引き,Rをとる QD:QP=QR:QC=5:8より,CR=4× AR=AC+CR=6+ |
||
| 3 | 立命館高校 (R6年) ★★ | 6 | 盈進高校 (R6年) ★★ |
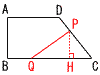 AD∥BC,∠A=90゜,AB=12cm,BC=24cm,AD=15cmの台形ABCDあります。 AD∥BC,∠A=90゜,AB=12cm,BC=24cm,AD=15cmの台形ABCDあります。(1) 点Pが点Cに到達するのは,点Pが動き出してから何秒後か求めなさい。 【解】CD=√122+92=15 (AD+DC)÷3=(15+15)÷3=10秒後 (2) 点Pが辺AD上にあるとき,2点P,Qが動き出してからx秒後の△PQCの面積を,xの式で表しなさい。 【解】底辺QC=24-2x, 高さは12 △PQC= (3) △PQCの面積が36/5cmとなるのは,何秒後か 【解】PがDC上のとき(5≦x≦10) PH= △PQC= (x-9)(x-13)=0で,5≦x≦10より, x=9秒後 |
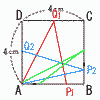 1辺が4cmの正方形ABCDがある。 1辺が4cmの正方形ABCDがある。(1) x=3のとき,yの値を求めなさい。 【解】AP1=3=1,Q1はDCの中点 y= (2) xの変域が4≦x≦6のとき,yをxの式で 【解】P2はBC上,Q2はDA上(AQ2=12-2x) y= (3) 点QがDを通過したあと,y=6を満たすxの値 【解】アにy=6を代入して,6=24-4xより, x= 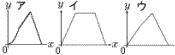 (4) もっともふさわしい (4) もっともふさわしい【解】 ア 0≦x≦2のとき, y= 2≦x≦4のとき,y= 4≦x≦6のとき,y= |
||