| 29 動点1 | 月 日( ) |
| 29 動点1 | 月 日( ) |
| 1 | 帝京高校 (R4年) ★★ | 4 | 鹿屋中央高校 (R4年) ★★ |
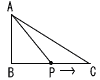 図のようなAB=6cm,BC=8cm,CA=10cmの直角三角形ABCにおいて,点Pは辺BC,CA上を点BからCを通り,Aまで毎秒2cmの速さで動く。点Pが点Bを出発してからx秒後の三角形ABPの面積をycm2とするとき, 図のようなAB=6cm,BC=8cm,CA=10cmの直角三角形ABCにおいて,点Pは辺BC,CA上を点BからCを通り,Aまで毎秒2cmの速さで動く。点Pが点Bを出発してからx秒後の三角形ABPの面積をycm2とするとき,(1) 0<x<4のとき,yをxの式で表しなさい。 (2) x=6のとき,yの値を求めなさい。 |
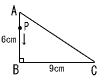 図のような,∠ABC=90°,AB=6cm,BC=9cmの直角三角形がある。頂点A上に点Pがあり,点Pは辺上をA→B→Cの順に毎秒1cmの速さで動き,点Pは頂点Cで止まる。 図のような,∠ABC=90°,AB=6cm,BC=9cmの直角三角形がある。頂点A上に点Pがあり,点Pは辺上をA→B→Cの順に毎秒1cmの速さで動き,点Pは頂点Cで止まる。(1) 点Pが頂点Aを出発してから4秒後のとき,△APCの面積を求めよ。 (2) △APCの面積が12cm2となるのは,点Pが頂点Aを出発してから何秒後か,すべて求めよ。 |
||
| 2 | 早稲田佐賀高校 (R4年) ★★★ | 5 | 就実高校 (R5年) ★★ |
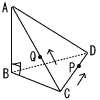 図のように,一辺の長さが3である正三角形BCDを底面とし,高さAB=3√3である三角すいABCDがある。点Pは辺CD,DB上を,C→D→B の順に,点Qは辺CA上を,C→Aにそれぞれ毎秒 1の速さで移動して,それぞれB,Aで止まる。 図のように,一辺の長さが3である正三角形BCDを底面とし,高さAB=3√3である三角すいABCDがある。点Pは辺CD,DB上を,C→D→B の順に,点Qは辺CA上を,C→Aにそれぞれ毎秒 1の速さで移動して,それぞれB,Aで止まる。(1) 三角すいABCDの体積V0を求めよ。 (2) P,QがCを同時に出発して1秒後の三角すいBCPQの体積V1を求めよ。 (3) P,QがCを同時に出発してt秒後(t>1)に,三角すいBCPQの体積が(2)のV1と等しくなった。このとき,tの値を求めよ。 |
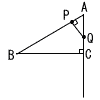 図のように,AB=10cm,BC=8cm,CA=6cmの直角三角形がある。点Pは,辺AB上を毎秒1cmの速さで点Aを出発して点Bまで動く。点Qは,点Pと同時に点Aを出発し,∠APQ=90°となるよう|こ半直線AC上を動く。 図のように,AB=10cm,BC=8cm,CA=6cmの直角三角形がある。点Pは,辺AB上を毎秒1cmの速さで点Aを出発して点Bまで動く。点Qは,点Pと同時に点Aを出発し,∠APQ=90°となるよう|こ半直線AC上を動く。(1) 点Pが点Aを出発して3秒後のとき,APの長さとAQの長さを求めなさい。 (2) 点Pが点Aを出発して6秒後のとき,線分PQと辺BCの交点をDとする。四角形APDCの面積を求めなさい。 (3) (2)のとき,線分AQ上に点Rを△APRと四角形APDCの面積が等しくなるようにとる。線分ARの長さを求めなさい。 |
||
| 3 | 立命館高校 (R6年) ★★ | 6 | 盈進高校 (R6年) ★★ |
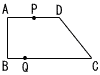 右の図のように,AD//BC,∠A=90゜,AB=12cm,BC=24cm,AD=15cmの台形ABCDあります。点Pは,点Aから点Dを通り,点Cまで毎秒3cmの速さで動きます。点Qは,点Bから点Cまで毎秒2cmの速さで動きます。2点P,Qがそれぞれ点Aと点Bから同時に動き出すとき,(ただし,2点P,Qは点Cに到達すると止まるものとします) 右の図のように,AD//BC,∠A=90゜,AB=12cm,BC=24cm,AD=15cmの台形ABCDあります。点Pは,点Aから点Dを通り,点Cまで毎秒3cmの速さで動きます。点Qは,点Bから点Cまで毎秒2cmの速さで動きます。2点P,Qがそれぞれ点Aと点Bから同時に動き出すとき,(ただし,2点P,Qは点Cに到達すると止まるものとします)(1) 点Pが点Cに到達するのは,点Pが動き出してから何秒後か求めなさい。 (2) 点Pが辺AD上にあるとき,2点P,Qが動き出してからx秒後の△PQCの面積を,xの式で表しなさい。 (3) △PQCの面積が36/5cmとなるのは,2点P,Qが動き出してから何秒後か求めなさい。 |
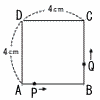 図のような1辺が4cmの正方形ABCDがある。点PはAを出発して,毎秒1cmの速さで辺AB上をBまで動き,その後は停止する。また,点QはBを出発して,毎秒2cmの速さで正方形の辺上をC,Dを通ってAまで動く。点P,Qが同時に出発してx秒後の△APQの面積をycm2とするとき, 図のような1辺が4cmの正方形ABCDがある。点PはAを出発して,毎秒1cmの速さで辺AB上をBまで動き,その後は停止する。また,点QはBを出発して,毎秒2cmの速さで正方形の辺上をC,Dを通ってAまで動く。点P,Qが同時に出発してx秒後の△APQの面積をycm2とするとき,(1) x=3のとき,yの値を求めなさい。 (2) xの変域が4≦x≦6のとき,yをxの式で表しなさい。 (3) 点QがDを通過したあと,y=6を満たすxの値を求めなさい。 (4) xとyの関係をグラフに表したとき,もっともふさわしいものを,次のア〜ウの中か 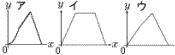 ら一つ選び,記号で答えなさい。 ら一つ選び,記号で答えなさい。 |
||