| ‚P | “Њ‹ћЌH‘е•Ќ‘®‰И‹ZЌ‚ЌZЃ@Ѓi‚q‚T”NЃjЃ@ЃљЃљ | ‚T | Љт•ЊЊ§—§Ќ‚ЌZЃ@Ѓi‚q‚S”NЃjЃ@ЃљЃљ | ||||||||||||
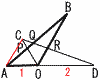 Ѓ@ЃўOAB‚р“_O‚р’†ђS‚Ж‚µ‚ДЋћЊv‰с‚и‚Й60Ѓ‹‚ѕ‚Ї‰с“]€Ъ“®‚і‚№‚Ѕ‚а‚М‚рЃўOCD‚Ж‚·‚йЃB Ѓ@ЃўOAB‚р“_O‚р’†ђS‚Ж‚µ‚ДЋћЊv‰с‚и‚Й60Ѓ‹‚ѕ‚Ї‰с“]€Ъ“®‚і‚№‚Ѕ‚а‚М‚рЃўOCD‚Ж‚·‚йЃB(1) ђь•ЄOR‚М’·‚і‚р‹Ѓ‚Я‚И‚і‚ўЃB Ѓy‰рЃzЃўAOC‚НђіЋOЉpЊ` ЃўDORЃдЃўDAC(‘ЉЋ—”д2:3) Ѓ@OR:ACЃЃDO:DA‚ж‚и,OR:1ЃЃ2:3‚Е, ORЃЃ (2) ’·‚і‚М”дAQ:QB‚рђ®ђ”‚М”д‚Е•\‚µ‚И‚і‚ўЃB Ѓy‰рЃzЃўQACЃдЃўQBR AQ:QBЃЃAC:BR=1:(2- (3) ’·‚і‚М”дAP:QR‚рђ®ђ”‚М”д‚Е•\‚µ‚И‚і‚ўЃB Ѓy‰рЃz ЃўACPЃдЃўBOP(‘ЉЋ—”д1:2)‚ж‚и,APЃЃ (2)‚ж‚и,QRЃЃ Ѓ@ABЃЃCD‚ѕ‚©‚з,ѓAѓC‚ж‚и, AP:QRЃЃ |
(1) ЃўABDЃдЃўCBE‚рЏШ–ѕ‚µ‚И‚і‚ўЃB ЃyЏШ–ѕЃzЃўABDЃдЃўCBE‚Е
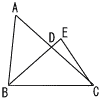 Ѓ@2Љp‘Љ“™‚ж‚и, ЃўABDЃдЃўCBE Ѓ@2Љp‘Љ“™‚ж‚и, ЃўABDЃдЃўCBE(2) ABЃЃ4cm,BCЃЃ5cm,CAЃЃ6cm ‡@ CE‚М’·‚і Ѓy‰рЃzЃўABC‚Е,BA:BCЃЃAD:CDЃЃ4:5 (6Ѓ|CD):CDЃЃ4:5‚ж‚и,CDЃЃ Ѓ@‚ж‚Б‚Д, CEЃЃCDЃЃ ‡A ЃўABD‚М–КђП‚Н,ЃўCDE‚М–КђП‚М‰Ѕ”{‚Е‚ ‚й‚© Ѓy‰рЃz(1)‚ж‚и,ЃўABD:ЃўCBEЃЃ42:52‚Е,ЃўCBEЃЃ ЃўCDEЃЃ Ѓ@‚ж‚Б‚Д, ЃўABDЃЃ |
||||||||||||||
| ‚Q | ‘еЌг•{—§Ќ‚ЌZBЃ@Ѓi‚q‚S”NЃjЃ@ЃљЃљ | ‚U | ђВ‰_Ќ‚ЌZЃ@Ѓi‚q‚S”NЃjЃ@ЃљЃљЃљ | ||||||||||||
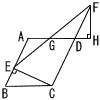 Ѓ@ЋlЉpЊ`ABCD‚Н•ЅЌsЋl•УЊ` Ѓ@ЋlЉpЊ`ABCD‚Н•ЅЌsЋl•УЊ`(1) ЃўBCEЃдЃўDFH‚Е‚ ‚й‚±‚Ж‚рЏШ–ѕ‚µ‚И‚і‚ўЃB ЃyЏШ–ѕЃzЃўBCE‚ЖЃўDFH‚Е,
(2) DHЃЃ2cm‚Е‚ ‚й‚Ж‚«, Ѓ@‡@ ђь•ЄBE‚М’·‚і‚р‹Ѓ‚Я‚И‚і‚ўЎ Ѓy‰рЃz(1)‚ж‚и,BE:2ЃЃ6:5‚Е,BEЃЃ Ѓ@‡AЃўFGD‚М–КђП‚р‹Ѓ‚Я‚И‚і‚ўЃB Ѓy‰рЃzЃўAEGЃдЃўDFG‚ж‚и,AEЃЃ7Ѓ| (6Ѓ|GD):GDЃЃ FHЃЃЃг21‚ж‚и,ЃўFGDЃЃ |
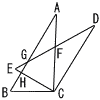 Ѓ@BCЃЃ2Ѓг2cm,ЃЪBACЃЃ30Ѓ‹ЃЪACBЃЃ90Ѓ‹‚МЃўABC‚Є‚ ‚йЃB Ѓ@BCЃЃ2Ѓг2cm,ЃЪBACЃЃ30Ѓ‹ЃЪACBЃЃ90Ѓ‹‚МЃўABC‚Є‚ ‚йЃB(1) ђь•ЄCF‚М’·‚і‚р‹Ѓ‚Я‚жЎ Ѓy‰рЃzЃўCEF‚НђіЋOЉpЊ` Ѓ@CFЃЃCEЃЃ2Ѓг2cm (2) ђь•ЄEH‚М’·‚і‚р‹Ѓ‚Я‚жЃB Ѓy‰рЃzЃўBCH‚Н,30,60,90“x Ѓ@CHЃЃ (3) ЃўGEH‚М–КЌВ‚р‹Ѓ‚Я‚жЎ Ѓy‰рЃzЃўEGHЃдЃўBCH GHЃЃЃг3(2Ѓг2Ѓ|Ѓг6)ЃЃЃг6(2Ѓ|Ѓг3)‚ж‚и, Ѓ@ЃўGEHЃЃ Ѓ@Ѓ@ЃЃ(7Ѓг3Ѓ|12)cm2 (4) ЋlЉpЊ`CFGH‚М–КђП‚р‹Ѓ‚Я‚жЃB Ѓy‰рЃzЃўCEFЃ|ЃўGEH |
||||||||||||||
| ‚R | ‹ЛЊхЉw‰ЂЌ‚ЌZЃ@Ѓi‚q‚U”NЃjЃ@ЃљЃљЃљ | ‚V | Џй–kЌ‚ЌZЃ@Ѓi‚q‚U”NЃjЃ@ЃљЃљ | ||||||||||||
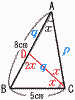 Ѓ@,•УAC‚М’·‚і‚р‹Ѓ‚Я‚жЃB Ѓ@,•УAC‚М’·‚і‚р‹Ѓ‚Я‚жЃBЃy‰рЃzЃЪC‚М“с“™•ЄђьCD‚р€ш‚‚Ж, 2Љp‘Љ“™‚ж‚и,ЃўABCЃдЃўCBD pЃЃAC,qЃЃADЃЃCD‚Ж‚·‚й‚Ж, Ѓ@AB:CBЃЃ‚`C:‚b‚c‚ж‚и,8:5ЃЃp:qЃcѓA Ѓ@CA:CBЃЃAD:BD‚ж‚и,p:5ЃЃq:(8Ѓ|q)ЃcѓC ѓAѓC‚ж‚и,pЃЃACЃЃ39/5 |
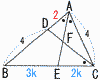 Ѓ@BE‚М’·‚і‚р‹Ѓ‚Я‚жЃB Ѓ@BE‚М’·‚і‚р‹Ѓ‚Я‚жЃBЃy‰рЃz ЃўACD‚Е,AC:ADЃЃ2:1‚ж‚и,ADЃЃ2 ЃўABC‚Е,BE:CEЃЃ6:4ЃЃ3:2 ‚±‚±‚Е,BEЃЃ3k,CEЃЃ2k‚Ж‚·‚й ЃўABEЃдЃўCBD‚ж‚и,6:5kЃЃ3k:4 Ѓ@15k2ЃЃ24‚ж‚и,kЃЃ |
||||||||||||||
| ‚S | ђ¬жьЌ‚ЌZЃ@Ѓi‚q‚U”NЃjЃ@ЃљЃљ | ‚W | ‘Ѓ‘еЌ‚“™Љw‰@Ѓ@Ѓi‚q‚U”NЃjЃ@Ѓљ | ||||||||||||
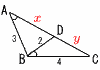 Ѓ@ђ}‚̂悤‚Й,ЃўABC‚М•УACЏг‚Й,ЃЪBACЃЃЃЪCBD‚Ж‚И‚й‚悤‚Й“_D‚р‚Ж‚йЃBABЃЃ3,BCЃЃ4,BDЃЃ2‚Е‚ ‚й‚Ж‚«,ђь•ЄAD‚М’·‚і‚р‹Ѓ‚Я‚жЃB Ѓ@ђ}‚̂悤‚Й,ЃўABC‚М•УACЏг‚Й,ЃЪBACЃЃЃЪCBD‚Ж‚И‚й‚悤‚Й“_D‚р‚Ж‚йЃBABЃЃ3,BCЃЃ4,BDЃЃ2‚Е‚ ‚й‚Ж‚«,ђь•ЄAD‚М’·‚і‚р‹Ѓ‚Я‚жЃBЃy‰рЃz2Љp‘Љ“™‚ж‚и,ЃўABCЃдЃўBDC
|
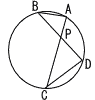 Ѓ@ђ}‚̂悤‚Й,‰~ЋьЏг‚Й4“_A,B,C,D‚Є‚ ‚йЃBђь•ЄAC‚Жђь•ЄBD‚МЊр“_‚рP‚Ж‚·‚йЃBABЃЃ3,BPЃЃx,CP ЃЃxЃ{2,CDЃЃxЃ{1‚Е‚ ‚й‚Ж‚«,x‚М’l‚р‹Ѓ‚Я‚жЃB Ѓ@ђ}‚̂悤‚Й,‰~ЋьЏг‚Й4“_A,B,C,D‚Є‚ ‚йЃBђь•ЄAC‚Жђь•ЄBD‚МЊр“_‚рP‚Ж‚·‚йЃBABЃЃ3,BPЃЃx,CP ЃЃxЃ{2,CDЃЃxЃ{1‚Е‚ ‚й‚Ж‚«,x‚М’l‚р‹Ѓ‚Я‚жЃBЃy‰рЃz2Љp‘Љ“™‚ж‚и,ЃўABPЃдЃўDCP 3:(xЃ{1)ЃЃx:(xЃ{2)‚р‰р‚ў‚Д, Ѓ@xЃЃ1Ѓ{Ѓг7 |
||||||||||||||