| �@�Q�@�����Ȑ}�` | �@�@�@���@�@�@���i�@�@�j |
| �@�Q�@�����Ȑ}�` | �@�@�@���@�@�@���i�@�@�j |
| �P | �����H�啍���ȋZ���Z�@�i�q�T�N�j�@���� | �T | �������Z�@�i�q�S�N�j�@���� |
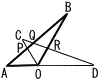 �@OA��1cm,OB��2cm,��AOB��120���́�OAB������B�}�̂悤��,��OAB��_O�𒆐S�Ƃ��Ď��v����60��������]�ړ����������̂���OCD�Ƃ���B��AB��OC�̌�_��P,AB��CD�̌�_��Q,OB��CD�̌�_��R�Ƃ���Ƃ�, �@OA��1cm,OB��2cm,��AOB��120���́�OAB������B�}�̂悤��,��OAB��_O�𒆐S�Ƃ��Ď��v����60��������]�ړ����������̂���OCD�Ƃ���B��AB��OC�̌�_��P,AB��CD�̌�_��Q,OB��CD�̌�_��R�Ƃ���Ƃ�,(1) ����OR�̒��������߂Ȃ����B (2) ����AQ��QB�̒����̔�AQ:QB�������Ƃ��ȒP�Ȑ����̔�ŕ\���Ȃ����B (3) ����AP��QR�̒����̔�AP:QR�������Ƃ��ȒP�Ȑ����̔�ŕ\���Ȃ����B �@ |
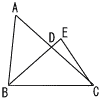 �@��ABC��,�_D�́�ABC�̓����ƕ�AC�Ƃ̌�_�ł���B�܂�,�_E�͐���BD�̉�������̓_��,CD��CE�ł��� �@��ABC��,�_D�́�ABC�̓����ƕ�AC�Ƃ̌�_�ł���B�܂�,�_E�͐���BD�̉�������̓_��,CD��CE�ł���(1) ��ABD�䁢CBE�ł��邱�Ƃ��ؖ����Ȃ����B (2) AB��4cm,BC��5cm,CA��6cm�̂Ƃ�, �@�@ CE�̒��������߂Ȃ����B �@�A ��ABD�̖ʐς�,��CDE�̖ʐς̉��{�ł��邩 �@�@�����߂Ȃ����B �@ |
||
| �Q | ���{�����ZB�@�i�q�S�N�j�@���� | �U | �_���Z�@�i�q�S�N�j�@������ |
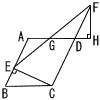 �@�l�p�`ABCD�͓��p��ABC���s�p�̕��s�l�ӌ`�ł���,AB��7cm,AD��6cm�ł���BE��,C�����AB�ɂЂ��������ƕ�AB�̌�_�ł���BF�͒���DC��ɂ�����D�ɂ���C�Ɣ��Α��ɂ���_�ł���,FD��5cm�ł���BE��F�Ƃ����ԁBG��,����EF�ƕ�AD�Ƃ̌�_�ł���BH��,F���璼��AD�ɂЂ��������ƒ���AD�Ƃ̌�_�ł���B �@�l�p�`ABCD�͓��p��ABC���s�p�̕��s�l�ӌ`�ł���,AB��7cm,AD��6cm�ł���BE��,C�����AB�ɂЂ��������ƕ�AB�̌�_�ł���BF�͒���DC��ɂ�����D�ɂ���C�Ɣ��Α��ɂ���_�ł���,FD��5cm�ł���BE��F�Ƃ����ԁBG��,����EF�ƕ�AD�Ƃ̌�_�ł���BH��,F���璼��AD�ɂЂ��������ƒ���AD�Ƃ̌�_�ł���B(1) ��BCE�䁢DFH�ł��邱�Ƃ��ؖ����Ȃ����B (2) DH��2cm�ł���Ƃ�, �@�@ ����BE�̒��������߂Ȃ���� �@�A��FGD�̖ʐς����߂Ȃ����B �@ |
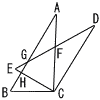 �@BC��2��2cm,��BAC��30����ACB��90���́�ABC������B��DEC��,��ABC��_C����]�̒��S�Ƃ��Ď��v�̐j�̉�]�Ɠ���������30����]�ړ��������̂ł���AC��DE,AB��DE,AB��CE�̌�_�����ꂼ��F,G,H�Ƃ���Ƃ�, �@BC��2��2cm,��BAC��30����ACB��90���́�ABC������B��DEC��,��ABC��_C����]�̒��S�Ƃ��Ď��v�̐j�̉�]�Ɠ���������30����]�ړ��������̂ł���AC��DE,AB��DE,AB��CE�̌�_�����ꂼ��F,G,H�Ƃ���Ƃ�,(1) ����CF�̒��������߂� (2) ����EH�̒��������߂�B (3) ��GEH�̖ʍ����߂� (4) �l�p�`CFGH�̖ʐς����߂�B �@ |
||
| �R | �ˌ��w�����Z�@�i�q�U�N�j�@������ | �V | ��k���Z�@�i�q�U�N�j�@���� |
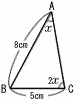 �@�}�̂悤�ȁ�ABC�ɂ�����,��C�̑傫���́�A�̑傫����2�{�ł���B���̂Ƃ�,��AC�̒��������߂�B �@�}�̂悤�ȁ�ABC�ɂ�����,��C�̑傫���́�A�̑傫����2�{�ł���B���̂Ƃ�,��AC�̒��������߂�B�@ |
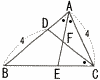 �@�E�̐}�̂悤�ɕ�AB��ɓ_D,��BC��ɓ_E���Ƃ�,AE��CD�̌�_��F�Ƃ���BAC��BD��4,��BAE����EAC����DCB,CF:FD��2:1�ł���Ƃ�,BE�̒��������߂�B �@�E�̐}�̂悤�ɕ�AB��ɓ_D,��BC��ɓ_E���Ƃ�,AE��CD�̌�_��F�Ƃ���BAC��BD��4,��BAE����EAC����DCB,CF:FD��2:1�ł���Ƃ�,BE�̒��������߂�B�@ |
||
| �S | �������Z�@�i�q�U�N�j�@���� | �W | ���卂���w�@�@�i�q�U�N�j�@�� |
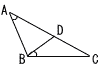 �@�}�̂悤��,��ABC�̕�AC���,��BAC����CBD�ƂȂ�悤�ɓ_D���Ƃ�BAB��3,BC��4,BD��2�ł���Ƃ�,����AD�̒��������߂�B �@�}�̂悤��,��ABC�̕�AC���,��BAC����CBD�ƂȂ�悤�ɓ_D���Ƃ�BAB��3,BC��4,BD��2�ł���Ƃ�,����AD�̒��������߂�B�@ |
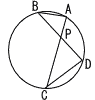 �@�}�̂悤��,�~�����4�_A,B,C,D������B����AC�Ɛ���BD�̌�_��P�Ƃ���BAB��3,BP��x,CP��x�{2,CD��x�{1�ł���Ƃ�,x�̒l�����߂�B �@�}�̂悤��,�~�����4�_A,B,C,D������B����AC�Ɛ���BD�̌�_��P�Ƃ���BAB��3,BP��x,CP��x�{2,CD��x�{1�ł���Ƃ�,x�̒l�����߂�B�@ |
||
�mTOP�n�mBACK�n�mNEXT�n�m���n�@�@���� �������� ��������@![]() ����p
����p