| �S�@�O�����̒藝�@�i�����j | ||
| �S�@�O�����̒藝�@�i�����j | ||
| �P | ���C��t���Y�����Z�@�i�q�T�N�j�@�� | �V | �]�ː�w����荂�Z�@�i�q�T�N�j�@���� | |||||||||||||||||||
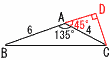 �@��ABC�̖ʐς�(�@�@)�ɂȂ�܂��B �@��ABC�̖ʐς�(�@�@)�ɂȂ�܂��B�y���z�i�E�}�Q�Ɓj ��DAC�͒��p�ӎO�p�`������, �@CD:4��1:��2��,CD��4/��2��2��2 �����, ��ABC�� |
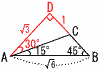 �@��BC�̒��������߂Ȃ����B �@��BC�̒��������߂Ȃ����B�y���z�i�E�}�Q�Ɓj ��DAB�͒��p�ӎO�p�`������, �@DA:��6��1:��2��,DA��DB����3 �܂�,DC��1���, BC����3�|1 |
|||||||||||||||||||||
| �Q | ��㋳��啍���r�c�Z�Ɂ@�i�q�S�N�j�@�� | �W | �ߋE�啍�����Z�@�i�q�S�N�j�@������ | |||||||||||||||||||
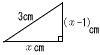 �@x�̒l�����߂Ȃ����B �@x�̒l�����߂Ȃ����B�y���zx2�{(x�|1)2��32 ��������, x2�|x�|4��0
|
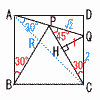 (1) ��PAB�̑傫�������߂�B (1) ��PAB�̑傫�������߂�B�y���z��ABP�Ł�B��30��, BA��BP �@��PAB��(180�|30)��2��75�� (2) ��BC�̒��������߂�B �y���z��QPH��180�|75�|60��45����, �@��QPH��,45,45,90����,PH��QH��1�c�A ��CQH��,30,60,90����,CH����3 �c�C �A�{�C���, BC��PC��1�{��3 (3) ����AP�̒��������߂�B �y���z��ADQ��,AQ2��(1�{��3)2�{(1�{��3�|2)2��8 �����, AP��2��2�|��2����2 (4) ����PR�̒��������߂�B �y���z��APR�䁢BAP(2�p����)���,
�y���z(2)���,AC����2(��3�{1)����6�{��2 �@CR��AC�|AR����6�{��2�|��2����6
|
|||||||||||||||||||||
| �R | ��㐯���w�@���Z�@�i�q�S�N�j�@���� | |||||||||||||||||||||
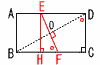 �@�܂�ڂ̒�����[�@�@]cm�ł���B �@�܂�ڂ̒�����[�@�@]cm�ł���B�y���z�i�E��}�Q�Ɓj �܂��EF��,�Ίp���̐������� BD����52�{122��13 ��DOFC��,��D����F�̊O�p E���琂��EH�����낷��, ��EHF�䁢BCD(2�p����) �@EF:13��5:12���, EF��13�~5��12��65/12 |
||||||||||||||||||||||
| �S | ����{�������w�@�@�i�q�S�N�j�@������ | |||||||||||||||||||||
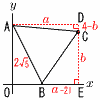 �@�萔a,b�̒l�����ꂼ�ꋁ�߂�B �@�萔a,b�̒l�����ꂼ�ꋁ�߂�B�y���z�i�E��}�Q�Ɓj AB����42�{22��2��5 ��ACD�Ɓ�CBE��, �@a2�{(4�|b)2��(a�|2)2�{b2��(2��5)2 ���̘A����������������,a��1�{2��3, b��2�{��3 |
||||||||||||||||||||||
| �T | �����w�@���Z�@�i�q�U�N�j�@�� | �X | �����V�����Z�@�i�q�U�N�j�@���� | |||||||||||||||||||
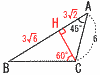 �@�}�̂悤�ȁ�ABC�̖ʐς����߂�B �@�}�̂悤�ȁ�ABC�̖ʐς����߂�B�y���z����CH�����낷 ��ACH��,AH��CH��6/��2��3��2 ��BCH��,BH����3CH��3��6 ��ABC�� |
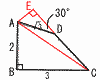 �@�}�̎l�p�`�̖ʐς����߂Ȃ����B �@�}�̎l�p�`�̖ʐς����߂Ȃ����B�y���z��ADE��30�� ��ADE��,AE�� �@��3�{( |
|||||||||||||||||||||
| �U | ���q�w�����Z�@�i�q�U�N�j�@������ | 10 | ��C��t�����Z�@�i�q�U�N�j�@���� | |||||||||||||||||||
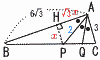 �@���p�O�p�`ABC������܂��B �@���p�O�p�`ABC������܂��B(1) �_P�����AB����PH�����낷�Ƃ�,PH �̒��������߂Ȃ����B �y���zPH��x�Ƃ����,BH��6��3�|��3x�c�A HP�aAC��,BH��6��3�~(x/3)��2��3x�c�C �A���C���,6��3�|��3x��2��3x��,x��PH��2 (2) BP�̒��������߂Ȃ����B �y���z ��BPH��,BP2��22�{(4��3)2���, BP��2��13 (3) ��APQ�̖ʐς����߂Ȃ����B �y���zBC��3��13���,PC����13��,PQ�� ��APQ����ABC�~(PQ/BC)��9��3�~ |
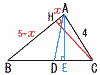 �@AB��5,BC��6,CA��4�ł���B �@AB��5,BC��6,CA��4�ł���B(1) AH�̒��������߂Ȃ����B �y���zAH��x,BH��5�|x�Ƃ����, CH2��42�|x2��62�|(5�|x)2��,x��AH�� (2) ��ABC�̖ʐς����߂Ȃ����B �y���zCH2��42�|�i ��ABC�� (3) AD�̒��������߂Ȃ����B �y���z(2)���,����AE�� ��ABE��,BE2��52�|( BD�� ��ADE��,AD2��( |
|||||||||||||||||||||