| 4 三平方の定理 | 月 日( ) |
| 4 三平方の定理 | 月 日( ) |
| 1 | 東海大付属浦安高校 (R5年) ★ | 7 | 江戸川学園取手高校 (R5年) ★★ |
 右の図の△ABCの面積は( )になります。 右の図の△ABCの面積は( )になります。 |
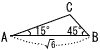 右の図のように,△ABCがあり,∠ABC=45°,∠BAC=15°,AB=√6のとき,辺BCの長さを求めなさい。 右の図のように,△ABCがあり,∠ABC=45°,∠BAC=15°,AB=√6のとき,辺BCの長さを求めなさい。 |
||
| 2 | 大阪教育大附属池田校舎 (R4年) ★ | 8 | 近畿大附属高校 (R4年) ★★★ |
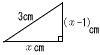 3辺が右の図のような直角三角形がある。xの値を求めなさい。 3辺が右の図のような直角三角形がある。xの値を求めなさい。 |
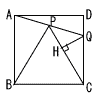 正方形ABCDの内部に点Pを△PBCが正三角形になるようにとる。直線APと辺CDの交点をQとし,Qから線分CPに垂線QHをひく。QH=1であるとき, 正方形ABCDの内部に点Pを△PBCが正三角形になるようにとる。直線APと辺CDの交点をQとし,Qから線分CPに垂線QHをひく。QH=1であるとき,(1) ∠PABの大きさを求めよ。 (2) 辺BCの長さを求めよ。 (3) 線分APの長さを求めよ。 (4) 線分ACと線分BPの交点をRとするとき,線分PRの長さを求めよ。 (5) △PRCの面積を求めよ。 |
||
| 3 | 大阪星光学院高校 (R4年) ★★ | ||
 AB=5cm,BC=12cmの長方形の紙ABCDをBとDが重なるように折ったとき,折り目の長さは[ ]cmである。 AB=5cm,BC=12cmの長方形の紙ABCDをBとDが重なるように折ったとき,折り目の長さは[ ]cmである。 |
|||
| 4 | 早大本庄高等学院 (R4年) ★★★ | ||
| 座標平面上に,2点A(0,4),B(2,0)がある。点C(a, b) を三角形ABCが正三角形になるようにとるとき,定数a,bの値をそれぞれ求めよ。ただし,a>0,b>0とする。 |
|||
| 5 | 明治学院高校 (R6年) ★★★ | 9 | 立教新座高校 (R6年) ★★★ |
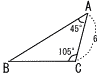 図のような△ABCの面積を求めよ。 図のような△ABCの面積を求めよ。 |
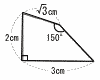 図の四角形の面積を求めなさい。 図の四角形の面積を求めなさい。 |
||
| 6 | 鎌倉学園高校 (R6年) ★★★ | 10 | 専修大付属高校 (R6年) ★★★ |
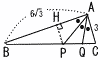 図のように,∠A=90°,AB=6√3,AC=3の直角三角形ABCがあります。∠Aを3等分する直線をAP,AQとします。 図のように,∠A=90°,AB=6√3,AC=3の直角三角形ABCがあります。∠Aを3等分する直線をAP,AQとします。(1) 点Pから辺ABへ垂線PHを下ろすとき,PH の長さを求めなさい。 (2) BPの長さを求めなさい。 (3) △APQの面積を求めなさい。 |
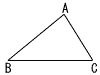 △ABCにおいて,AB=5,BC=6,CA=4である。∠Aの二等分線と辺BCの交点をDとする。また,点Cから辺ABに引いた垂線とABとの交点をHとする。 △ABCにおいて,AB=5,BC=6,CA=4である。∠Aの二等分線と辺BCの交点をDとする。また,点Cから辺ABに引いた垂線とABとの交点をHとする。(1) AHの長さを求めなさい。 (2) △ABCの面積を求めなさい。 (3) ADの長さを求めなさい。 |
||