 図形 |
５ 中心角・円周角 （略解） | |
| 図形 |
５ 中心角・円周角 （略解） | |
| １ | 愛知県立高校 （Ｒ５年） ★ | ７ | 大阪教育大附属平野校舎 （Ｒ５年） ★ | ||||||
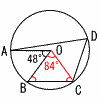 ∠AOB＝48°のとき,∠ADCの大きさは( )度である。【解】 △OBCで,∠B＝∠C＝48°より,∠BOC＝84° よって, ∠ADC＝(48＋84)÷2＝66° |
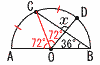 ∠ABC＝36°のとき,∠xの大きさを求めなさい。【解】OとCを結ぶ ∠AOC＝∠COD＝72°より,∠BOD＝36° よって,∠x＝180−(36＋36)＝108° |
||||||||
| ２ | 明治学院高校 （Ｒ４年） ★★ | ８ | 東京工大附属科技高校 （Ｒ５年） ★ | ||||||
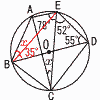 ∠xの大きさを求めなさい。【解】右図参照 △EBDは直角三角形だから, ∠EBD＝35°  ABDEは円に内接するから,∠B＋∠E＝180°∠x＝180−(78＋52＋35)＝15° |
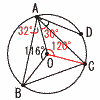 図において,4点A,B,C,Dは円Oの周上にある。∠BAD＝80°,∠ABC＝60°,∠AOB＝116°であるとき,∠CADの大きさを求めなさい。【解】OとCを結ぶ △OABで,∠OAB＝(180−116)÷2＝32° △OACで,∠OAC＝(180−120)÷2＝30° よって,∠CAD＝80−(32＋30)＝18° |
||||||||
| ３ | 土浦日大高校 （Ｒ４年） ★★ | ９ | 中央大杉並高校 （Ｒ４年） ★★ | ||||||
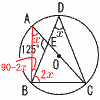 ∠xの大きさを求めなさい。【解】右図参照 ∠DBC＝2x(円周角に比例) △ABCで,x＋(90−2x)＋125＝180 これを解いて, ∠x＝35° |
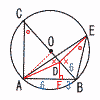 半径9の円Oがあります。弦ABの長さを9に,点Dを直径BC上にBD:DC＝1:2となるようにとります。また,線分ADをDの方へ延長した直線と,円Oとの交点をEとします。さらに,点Aと点C,点Bと点Eをそれぞれ結ぶ線分をひくとき,(1) 点Dから線分ABにおろした垂線の長さを求めなさい。 【解】右図参照 △DFBで,∠B＝60°DB＝18×  ＝6DF＝  DB＝DB＝×6＝3√3(2) 線分AEの長さを求めなさい。 【解】右上図参照 2角相等より,△BED∽△ACDで,AD:BD＝CD:ED AF＝9−3＝6より,AD＝√62＋(3√3)2＝3√7 3√7:6＝12:EDで,ED＝(24/7)√7
|
||||||||
| ４ | 日大第二高校 （Ｒ４年） ★★ | ||||||||
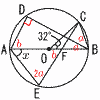 ∠xの大きさを求めなさい。【解】右図参照 △OBCで,a＝(180−32)÷4＝37° △DABで,b＝90−37＝53° △AEFで,∠x＝180−(2a＋b)＝180−127＝53° |
|||||||||
| ５ | 埼玉県立高校 （Ｒ６年） ★ | 10 | 玉川学園高等部 （Ｒ６年） ★ | ||||||
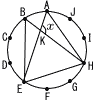 ∠AKHの大きさxを求めなさい。【解】△AKHで ∠A＝360×  × ＝54°∠H＝360×  ×＝18°x＝180−(54＋18)＝108° |
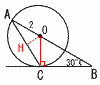 線分ACの長さを求めよ。【解】垂線OCを下ろす △OACで,∠A＝∠C＝30° AH＝CH＝√3より, AC＝2√3cm |
||||||||
| ６ | 江戸川学園取手高校 （Ｒ６年） ★ | 11 | 大阪星光学院高校 （Ｒ６年） ★★ | ||||||
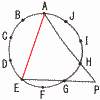 ∠APEの大きさを求めなさい。【解】円周角は弧の長さに比例 ∠A＝360× ×＝54°∠E＝360×× ＝72°∠APE＝180−(54＋72)＝54° |
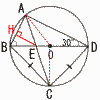 円の半径は[ ]で,CE＝[ ]である。【解】△ABEで,垂線EHを下ろす AH＝EH＝√6÷√2＝√3, BH＝1 △OABは正三角形だから,半径＝AB＝√3＋1 △BCDで,CD＝√2OD＝√2AB, またBE＝2 △ABE∽△DCE(比1:√2)より,CE＝√2BE＝2√2 |
||||||||