| ‚UЃ@‰~‚ЖЋOЉpЊ`Ѓ@Ѓi—Є‰рЃj | ||
| ‚UЃ@‰~‚ЖЋOЉpЊ`Ѓ@Ѓi—Є‰рЃj | ||
| ‚P | –ѕЋЎЉw‰@Ќ‚ЌZЃ@Ѓi‚q‚S”NЃjЃ@ЃљЃљЃљ | ‚R | “ЇЋuЋРЌ‚ЌZЃ@Ѓi‚q‚S”NЃjЃ@ЃљЃљЃљ | |||||||||||||||||
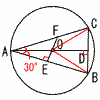 Ѓ@“_O‚р’†ђS‚Ж‚·‚й”јЊa2‚М‰~‚ЙABЃЃAC,ЃЪA‚Є‰sЉp‚М“с“™•УЋOЉpЊ`ABC‚Є“ађЪ‚µ‚Д‚ў‚йЃB Ѓ@“_O‚р’†ђS‚Ж‚·‚й”јЊa2‚М‰~‚ЙABЃЃAC,ЃЪA‚Є‰sЉp‚М“с“™•УЋOЉpЊ`ABC‚Є“ађЪ‚µ‚Д‚ў‚йЃB(1) ђь•ЄBD‚М’·‚і‚р‹Ѓ‚Я‚жЃB Ѓy‰рЃzЃi‰EЏгђ}ЋQЏЖЃj ЃўOBD‚Е, BDЃЃЃг22Ѓ|(Ѓг3)2ЃЃ1 (2) AE2‚М’l‚р‹Ѓ‚Я‚жЃB Ѓy‰рЃzЃўAOEЃдЃўABD(2Љp‘Љ“™)‚ж‚и, Ѓ@2:2AEЃЃAE:(2Ѓ{Ѓг3)‚ж‚и,AE2ЃЃ2Ѓ{Ѓг3 (3) ЃўAEF‚М–КђП‚р‹Ѓ‚Я‚жЃB Ѓy‰рЃzЃўOBC‚НђіЋOЉpЊ`‚ѕ‚©‚з,ЃЪAЃЃ30Ѓ‹
|
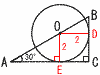
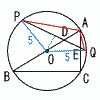 Ѓ@ђь•ЄPQ‚Жђь•ЄAB,AC‚Ж‚МЊр“_‚р‚»‚к‚ј‚кD,E‚Ж‚·‚й‚Ж‚«, Ѓ@ђь•ЄPQ‚Жђь•ЄAB,AC‚Ж‚МЊр“_‚р‚»‚к‚ј‚кD,E‚Ж‚·‚й‚Ж‚«,Ѓy‰рЃzЃi‰Eђ}ЋQЏЖЃj (1) ЃЪPAQ‚М‘е‚«‚і‚р‹Ѓ‚Я‚жЃB ЃўAPQ‚Е,ЃЪPЃЃ Ѓ@ЃЪQЃЃ Ѓ@‚ж‚Б‚Д,ЃЪPAQЃЃ180Ѓ|15Ѓ|45ЃЃ120Ѓ‹ (2) ђь•ЄPQ‚М’·‚і‚р‹Ѓ‚Я‚жЃB ЃЪAOPЃЃ2ЃЪAQPЃЃ45Ѓ~2ЃЃ90Ѓ‹ ЃЪAOQЃЃ2ЃЪAPQЃЃ15Ѓ~2ЃЃ30Ѓ‹ ЃўOPQ‚Н,120,30,30Ѓ‹PQЃЃ5Ѓг3cm (3) ђь•ЄDE‚М’·‚і‚р‹Ѓ‚Я‚жЃB ЃўOPD‚Е,ODЃЃ5/Ѓг3ЃЃ
|
|||||||||||||||||||
| ‚Q | ђВ‰_Ќ‚ЌZЃ@Ѓi‚q‚T”NЃjЃ@ЃљЃљ | ‚S | “Њ‘еЋ›Љw‰ЂЌ‚ЌZЃ@Ѓi‚q‚S”NЃjЃ@ЃљЃљЃљ | |||||||||||||||||
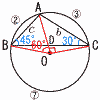 Ѓ@’†ђSO‚М‰~‚Й“ађЪ‚·‚йЃўABC‚Й‚В‚ў‚Д, Ѓ@’†ђSO‚М‰~‚Й“ађЪ‚·‚йЃўABC‚Й‚В‚ў‚Д,(1) b‚р,c‚р—p‚ў‚Д•\‚№ЃB Ѓy‰рЃz’†ђSЉp‚НЊК‚М’·‚і‚Й”д—б‚·‚й‚©‚з, ЃЪAOBЃЃ60Ѓ‹,ЃЪAOCЃЃ90Ѓ‹ ЃўOAC‚Н’јЉp“с“™•УЋOЉpЊ` 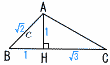 Ѓ@OAЃЃOC=c‚ж‚и, bЃЃЃг2c Ѓ@OAЃЃOC=c‚ж‚и, bЃЃЃг2c(2) a‚р,c‚р—p‚ў‚Д•\‚№ЃB Ѓy‰рЃzЃўABC‚Е,ђ‚ђьAH‚р‚Ё‚л‚· ЃЪBЃЃ45Ѓ‹,ЃЪCЃЃ30Ѓ‹
(3) ‰~‚М”јЊa‚рR,’јђьAO‚Ж’јђьBC‚МЊр“_‚рD‚Ж‚·‚й‚Ж‚«,AD‚М’·‚і‚ЖBC‚М’·‚і‚МђП‚р,R‚р—p‚ў‚Д•\‚№ЃB Ѓy‰рЃz ЃўADC‚Е,ЃЪADCЃЃ180Ѓ|45Ѓ|30ЃЃ105Ѓ‹ ЃўADCЃдЃўBAC‚ж‚и, AD:ACЃЃBA:BC‚Е, Ѓ@ADЃ~BCЃЃACЃ~BAЃЃЃг2RЃ~RЃЃЃг2R2 Ѓ@ |
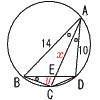 (1) ђь•ЄDE‚М’·‚і‚р‹Ѓ‚Я‚жЃB (1) ђь•ЄDE‚М’·‚і‚р‹Ѓ‚Я‚жЃBЃy‰рЃzЃi‰EЏгђ}ЋQЏЖЃj ЃўABD‚Е,BE:DEЃЃAB:ADЃЃ7:5 Ѓ@DEЃЃ (2) ђь•ЄBC‚М’·‚і‚р‹Ѓ‚Я‚жЃB Ѓy‰рЃzAEЃЃx,ECЃЃy‚Ж‚·‚й‚Ж, ЃўBECЃдЃўAED‚ж‚и, Ѓ@ ЃўABCЃдЃўAED‚ж‚и, Ѓ@14:(xЃ{y)ЃЃx:10‚Е,x2Ѓ{xyЃЃ140ЃcѓC 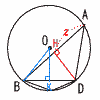 ѓA‚рѓC‚Й‘г“ь‚µ‚Д,xЃЃ ѓA‚рѓC‚Й‘г“ь‚µ‚Д,xЃЃ
Ѓy‰рЃzђ‚ђьDO‚Е,AHЃЃz‚Ж‚·‚й‚Ж, ЃўABD‚Е,102Ѓ|z2ЃЃ(6Ѓг2)2Ѓ|(14Ѓ|z)2 Ѓ@‚±‚к‚р‰р‚ў‚Д,zЃЃ8‚Е,DHЃЃ6 BD‚М’†“_K‚р‚Ж‚й‚Ж,ЃўOKBЃдЃўAHD‚Е, Ѓ@OBЃЃ |
|||||||||||||||||||
| ђ¬ЏйЉw‰ЂЌ‚ЌZЃ@Ѓi‚q‚U”NЃjЃ@Ѓљ | ‘Ѓ‘е–{ЏЇЌ‚“™Љw‰@Ѓ@Ѓi‚q‚U”NЃjЃ@ЃљЃљ | |||||||||||||||||||
 Ѓ@‰E‚Мђ}‚̂悤‚И’јЉpЋOЉpЊ`‚`BC‚Є‚ ‚и,“с•УAC,BC‚Н”јЊa2‡p‚М‰~O‚ЙђЪ‚µ‚Д‚ў‚йЃBAC‚М’·‚і‚р‹Ѓ‚Я‚жЃB Ѓ@‰E‚Мђ}‚̂悤‚И’јЉpЋOЉpЊ`‚`BC‚Є‚ ‚и,“с•УAC,BC‚Н”јЊa2‡p‚М‰~O‚ЙђЪ‚µ‚Д‚ў‚йЃBAC‚М’·‚і‚р‹Ѓ‚Я‚жЃBЃy‰рЃzЃўOAE‚Е,AEЃЃ2Ѓг3 Ѓ@‚ж‚Б‚Д,ACЃЃ(2Ѓг3Ѓ{2)cm |
 Ѓ@ЃЪBACЃЃa‚Ж‚·‚й‚Ж‚«,ЃЪDABЃ{ЃЪDBAЃ{ЃЪEACЃ{ЃЪECA‚рa‚р—p‚ў‚Д•\‚№ЃB Ѓ@ЃЪBACЃЃa‚Ж‚·‚й‚Ж‚«,ЃЪDABЃ{ЃЪDBAЃ{ЃЪEACЃ{ЃЪECA‚рa‚р—p‚ў‚Д•\‚№ЃBЃy‰рЃz Ѓ@ЃЪAЃ{ЃЪBЃЃ(xЃ{aЃ{z)Ѓ{(yЃ{x)ЃЃ180Ѓ‹ —^Ћ®ЃЃxЃ{yЃ{zЃ{xЃЃ(180Ѓ|a)Ѓ‹ |
|||||||||||||||||||
ЃmTOPЃnЃ@Ѓm–в‘и‚Й‚а‚З‚йЃnЃ@Ѓ@ЃљЃ@’†Ѓ@Ѓ@ЃљЃљЃ@‚в‚в“пЃ@Ѓ@ЃљЃљЃљЃ@“п