| 6 円と三角形 | 月 日( ) |
| 6 円と三角形 | 月 日( ) |
| 1 | 明治学院高校 (R4年) ★★★ | 4 | 同志社高校 (R4年) ★★★ |
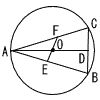 点Oを中心とする半径2の円にAB=AC,∠Aが鋭角の二等辺三角形ABCが内接している。直線AOと辺BCの交点をDとすると,OD=√3である。辺ABの中点をE,直線EOと辺ACの交点をFとする。 点Oを中心とする半径2の円にAB=AC,∠Aが鋭角の二等辺三角形ABCが内接している。直線AOと辺BCの交点をDとすると,OD=√3である。辺ABの中点をE,直線EOと辺ACの交点をFとする。(1) 線分BDの長さを求めよ。 (2) AE2の値を求めよ。 (3) △AEFの面積を求めよ。 |
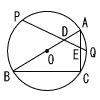 半径5cmの円Oがあり,円周上の3点A,B,Cを頂点とする△ABCは,∠A=60°,∠B=30°の直角三角形である。円Oの点Cを含まない側の弧ABの中点をP,点Bを含まない側の弧ACの中点をQとする。線分PQと線分AB,ACとの交点をそれぞれD,Eとするとき, 半径5cmの円Oがあり,円周上の3点A,B,Cを頂点とする△ABCは,∠A=60°,∠B=30°の直角三角形である。円Oの点Cを含まない側の弧ABの中点をP,点Bを含まない側の弧ACの中点をQとする。線分PQと線分AB,ACとの交点をそれぞれD,Eとするとき,(1) ∠PAQの大きさを求めよ。 (2) 線分PQの長さを求めよ。 (3) 線分DEの長さを求めよ。 |
||
| 2 | 青雲高校 (R5年) ★★ | 5 | 東大寺学園高校 (R4年) ★★★ |
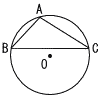 中心Oの円に内接する△ABCについて, 中心Oの円に内接する△ABCについて,(1) bを,cを用いて表せ。 (2) aを,cを用いて表せ。 (3) 円の半径をR,直線AOと直線BCの交点をDとするとき,ADの長さとBCの長さの積を,Rを用いて表せ。 |
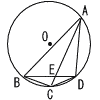 円Oの周上に4点,A,B,C,Dがあり,AB=14,AD=10,BD=6√2,∠BAC=∠DACを満たしている。 円Oの周上に4点,A,B,C,Dがあり,AB=14,AD=10,BD=6√2,∠BAC=∠DACを満たしている。(1) 線分ACと線分BDの交点をEとするとき,線分DEの長さを求めよ。 (2) 線分BCの長さを求めよ。 (3) 円Oの半径を求めよ。 |
||
| 3 | 成城高校 (R6年) ★★★ | 6 | 早大本庄高等学院 (R6年) ★★★ |
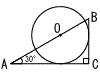 右の図のような直角三角形ABCがあり,二辺AC,BCは半径2㎝の円Oに接している。ACの長さを求めよ。 右の図のような直角三角形ABCがあり,二辺AC,BCは半径2㎝の円Oに接している。ACの長さを求めよ。 |
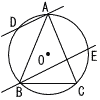 図において,AB=ACである二等辺三角形ABCは円Oに内接し,円周上の点D,EをAD∥EBとなるようにとる。∠BAC=aとするとき,∠DAB+∠DBA+∠EAC+∠ECAをaを用いて表せ。 図において,AB=ACである二等辺三角形ABCは円Oに内接し,円周上の点D,EをAD∥EBとなるようにとる。∠BAC=aとするとき,∠DAB+∠DBA+∠EAC+∠ECAをaを用いて表せ。 |
||