| ‚VЃ@‰~‚ЖҺlЉpЊ`Ѓ@Ѓi—Ғ‰рЃj | ||
| ‚VЃ@‰~‚ЖҺlЉpЊ`Ѓ@Ѓi—Ғ‰рЃj | ||
| ‚P | “ъ‘еЏKҺu–мҚ‚ҚZЃ@Ѓi‚q‚S”NЃjЃ@ЃљЃљ | ‚S | ђ_“ЮђмЊ§—§Қ‚ҚZЃ@Ѓi‚q‚S”NЃjЃ@ЃљЃљЃљ | ||||||||||||
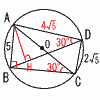 Ѓ@ҺlЉpЊ`ABCD‚ҒAC‚р’әЊa‚Ж‚·‚й”әЊa5cm‚М‰~O‚Й“ађЪ‚µ‚Д‚ұ‚йЃB Ѓ@ҺlЉpЊ`ABCD‚ҒAC‚р’әЊa‚Ж‚·‚й”әЊa5cm‚М‰~O‚Й“ађЪ‚µ‚Д‚ұ‚йЃBЃ@ABЃЃ5cm,CDЃЃ2Ѓг5cm‚М‚Ж‚«,ЃЪADBЃЃ[Ѓ@Ѓ@]“x,BDЃЃЃгЃ@(Ѓ@Ѓ@Ѓ@)cm‚Е‚ ‚йЃB Ѓy‰рЃzЃұABC‚Е, ЃЪBЃЃ90Ѓ‹,ABЃЃ5,ACЃЃ10‚ж‚и Ѓ@ЃЪACBЃЃ30Ѓ‹‚ң‚©‚з, Ѓ@Ѓ@ЃЪADBЃЃЃЪACBЃЃ30“x 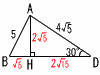 ЃұACD‚Е,ADЃЃЃг102Ѓ|(2Ѓг5)2ЃЃ4Ѓг5 ЃұABD‚Е,ђ‚ђьAH‚р‰ғ‚л‚·‚Ж, Ѓ@AHЃЃ2Ѓг5,DHЃЃ2Ѓг15,BHЃЃЃг5 BDЃЃЃг5Ѓ{2Ѓг15ЃЃЃг5(1Ѓ{2Ѓг3)cm |
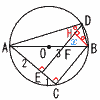 Ѓ@ђь•ҒAB‚Н‰~O‚М’әЊa‚Е‚ ‚и,2“_C,D‚Н‰~O‚МҺьЏг‚М“_‚Е‚ ‚йЃB Ѓ@ђь•ҒAB‚Н‰~O‚М’әЊa‚Е‚ ‚и,2“_C,D‚Н‰~O‚МҺьЏг‚М“_‚Е‚ ‚йЃBЃ@‚Ь‚Ң,“_E‚Нђь•ҒACЏг‚М“_‚Е,BCЃaDE‚Е‚ ‚и,“_F‚Нђь•ҒAB‚Жђь•ҒDE‚Ж‚МЊр“_‚Е‚ ‚йЃB Ѓ@AEЃЃ2cm,CEЃЃ1cm,DEЃЃ3cm‚М‚Ж‚«,ҺOЉpЊ`BDF‚М–КђП‚Н[Ѓ@Ѓ@]cm2‚Е‚ ‚йЃB Ѓy‰рЃzђ‚ђьBH‚р‚Ё‚л‚·‚Ж,BHЃЃ1 ЃұAEDЃдЃұBHD(2Љp‘Љ“™)‚Е,DHЃЃ ЃұAEFЃдЃұBHFЃi‘ЉҺ—”д2:1Ѓj Ѓ@FHЃЃx‚Ж‚·‚й‚Ж,EF:HFЃЃ( Ѓ@‚±‚к‚р‰р‚ұ‚Д, xЃЃ ЃұBDFЃЃ |
||||||||||||||
| ‚Q | “Њ‘еҺ›Љw‰ЂҚ‚ҚZЃ@Ѓi‚q‚T”NЃjЃ@ЃљЃљЃљ | ‚T | ѓ‰ЃEѓTЃ[ѓ‹Қ‚ҚZЃ@Ѓi‚q‚S”NЃjЃ@ЃљЃљЃљ | ||||||||||||
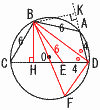 Ѓ@ђ}‚̂悤‚Й,“_O‚р’†ђS‚Ж‚·‚й‰~‚O‚МҺьЏг‚Й4“_A,B,C,D‚Ғ‚ ‚и,ABЃЃBCЃЃ6,CDЃЃ10,DAЃЃ4‚р–һ‚Ң‚µ‚Д‚ұ‚йЃB Ѓ@ђ}‚̂悤‚Й,“_O‚р’†ђS‚Ж‚·‚й‰~‚O‚МҺьЏг‚Й4“_A,B,C,D‚Ғ‚ ‚и,ABЃЃBCЃЃ6,CDЃЃ10,DAЃЃ4‚р–һ‚Ң‚µ‚Д‚ұ‚йЃB(1) ЃұABD‚М–КђП‚ЖЃұBCD‚М–КђП‚М”д‚рҚЕ‚аЉИ’P‚Иђ®ђ”‚М”д‚Е•\‚№ЃB Ѓy‰рЃzDB‚НЃЪKDC‚М“с“™•Ғђь BKЃЃBH‚ж‚и,ЃұABD:ЃұBCDЃЃAD:CDЃЃ2:5 (2) ђь•ҒCDЏг‚ЙCEЃЃ6‚Ж‚И‚й“_E‚р‚Ж‚й‚Ж‚«,ЃұBED‚М–КђП‚р‹Ѓ‚Я‚жЃB Ѓy‰рЃzЃұABDЃЯЃұEBD‚Е,BEЃЃ6 ЃұBCE‚Н1•У6‚МђіҺOЉpЊ`‚Е,BHЃЃ3Ѓг3 Ѓ@ЃұBEDЃЃ (3) ђь•ҒBD‚М’·‚і‚р‹Ѓ‚Я‚жЃB Ѓy‰рЃzЃұBHD‚Е BDЃЃЃг(3Ѓг3)2Ѓ{72ЃЃ2Ѓг19 (4) ‰~‚O‚М”әЊa‚р‹Ѓ‚Я‚жЃB Ѓy‰рЃzЃұBDF‚М“аЉp‚Н,30,60,90Ѓ‹
|
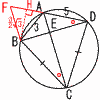 Ѓ@‰~‚Й“ађЪ‚·‚йҺlЉpЊ`ABCD‚НABЃЃ3,BCЃЃCD,DAЃЃ5,ЃЪBCDЃЃ60Ѓ‹‚р–һ‚Ң‚µ‚Д‚ұ‚йЃB Ѓ@‰~‚Й“ађЪ‚·‚йҺlЉpЊ`ABCD‚НABЃЃ3,BCЃЃCD,DAЃЃ5,ЃЪBCDЃЃ60Ѓ‹‚р–һ‚Ң‚µ‚Д‚ұ‚йЃB(1) ‘ОЉpђьAC,BD‚М’·‚і Ѓy‰рЃz ђіЃұABF‚Йђ‚ђьDH‚р‚Ж‚й‚Ж, Ѓ@ЃұBDH‚Е, BDЃЃЃг{( ЃұABCЃЯЃұFBD‚ж‚и, ACЃЃFDЃЃ3Ѓ{5ЃЃ8 (2) AC‚ЖBD‚МЊр“_‚рE‚Ж‚µ‚Д, Ѓ@Ѓ@Ѓ@ђь•Ғ‚М’·‚і‚М”дAE:EC Ѓy‰рЃz ЃұAEDЃдЃұFBD(‘ЉҺ—”д5:8)‚ж‚и, Ѓ@AEЃЃ3Ѓ~ ‚ж‚Б‚Д, AE:ECЃЃ |
||||||||||||||
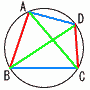 [ҺQҚl]ѓgѓЊѓ~Ѓ[‚М’и—қ [ҺQҚl]ѓgѓЊѓ~Ѓ[‚М’и—қЃ@ABЃ~CDЃ{ADЃ~BCЃЃACЃ~BD Ѓ@(Қ¶Ѓ~‰EЃ{ЏгЃ~‰ғЃЃ‘ОЉpђь‚З‚¤‚µ) Џг‚М(1)‚Е‚Н Ѓ@3Ѓ~7Ѓ{5Ѓ~7ЃЃ8Ѓ~7Ѓ@‚Ғђ¬‚и—§‚В |
|||||||||||||||
| ‚R | ”џЉЩѓ‰ЃEѓTЃ[ѓ‹Қ‚ҚZЃ@Ѓi‚q‚U”NЃjЃ@ЃљЃљ | (2) DC‚М’·‚і‚р‹Ѓ‚Я‚И‚і‚ұЃB Ѓy‰рЃzABЃaDC‚ж‚и, ЃұABDЃдЃұADE(”д 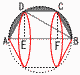 DCЃЃABЃ|2AEЃЃ DCЃЃABЃ|2AEЃЃ(3) ‰E‚Мђ}‚Н,‘дЊ`ABCD‚Ж‚»‚М‘дЊ`‚ЙЉOђЪ‚µ‚Д‚ұ‚й‰~‚М€к•”‚Е‚ ‚йЃBђ}‚МҺОђь•”•Ғ‚р’әђьAB‚рҺІ‚Й1‰с“]‚µ‚Д‚Е‚«‚й‰с“]‘М‚М‘МђП‚р ‹Ѓ‚Я‚И‚і‚ұЃB Ѓy‰рЃz‰с“]‘МЃЃ‹…Ѓ|Қ¶‰E‚М‰~ђҚЃ|’†‰›‚М‰~’Њ Ѓ@ЃЃ Ѓ@ЃЃ500/81ѓОЃ|125/108ѓОЃ|125/36ѓОЃЃ125/81ѓО |
|||||||||||||
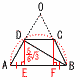 Ѓ@ABЃЃ Ѓ@ABЃЃ(1) ЃЪADB‚М‘е‚«‚і‚р‹Ѓ‚Я‚И‚і‚ұЃB Ѓy‰рЃzЃұABD‚Е, AD2Ѓ{BD2ЃЃ( AB2ЃЃ ( ѓAЃЃѓC‚ж‚и, AD2Ѓ{BD2ЃЃ AB2‚Е,ЃЪADBЃЃ90Ѓ‹ Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@(‰E‚ւ‚ÂЃЁ) |
|||||||||||||||
ЃmTOPЃnЃ@Ѓm–в‘и‚Й‚а‚З‚йЃnЃ@Ѓ@ЃљЃ@’†Ѓ@Ѓ@ЃљЃљЃ@‚в‚в“пЃ@Ѓ@ЃљЃљЃљЃ@“п