 図形 |
７ 円と四角形 | 月 日（ ） |
| 図形 |
７ 円と四角形 | 月 日（ ） |
| １ | 日大習志野高校 （Ｒ４年） ★★ | ４ | 神奈川県立高校 （Ｒ４年） ★★★ |
| 四角形ABCDがACを直径とする半径5cmの円Oに内接している。 AB＝5cm,CD＝2√5cmのとき,∠ADB＝[ ]度, BD＝√ ( )cmである。  |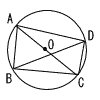
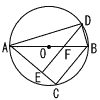 線分ABは円Oの直径であり,2点C,Dは円Oの周上の点である。また,点Eは線分AC上の点で,BC∥DEであり,点Fは線分ABと線分DEとの交点である。 AE＝2cm,CE＝1cm,DE＝3cmのとき,三角形BDFの面積は[ ]cm2である。 |
||
| ２ | 東大寺学園高校 （Ｒ５年） ★★★ | ５ | ラ・サール高校 （Ｒ４年） ★★★ |
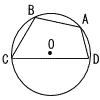 図のように,点Oを中心とする円０の周上に4点A,B,C,Dがあり,AB＝BC＝6,CD＝10,DA＝4を満たしている。(1) △ABDの面積と△BCDの面積の比を最も簡単な整数の比で表せ。 (2) 線分CD上にCE＝6となる点Eをとるとき,△BEDの面積を求めよ。 (3) 線分BDの長さを求めよ。 (4) 円０の半径を求めよ。 |
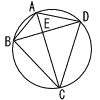 円に内接する四角形ABCDはAB＝3,BC＝CD,DA＝5,∠BCD＝60°を満たしている。このとき,次を求めよ。 (1) 対角線AC,BDの長さ (2) ACとBDの交点をEとして,線分の長さの比AE:EC |
||
| ３ | 函館ラ・サール高校 （Ｒ６年） ★★ | (2) DCの長さを求めなさい。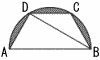 (3) 右の図は,台形ABCDとその台形に外接している円の一部である。図の斜線部分を直線ABを軸に1回転してできる回転体の体積を 求めなさい。 |
|
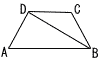 AB＝ ㎝,AD＝ ㎝,BD＝√3㎝である台形ABCD（AB∥DC）がある。この台形が円に内接している。(1) ∠ADBの大きさを求めなさい。 (右へつづく→) |
|||
