 図形 |
８ 円と接線 （略解） | |
| 図形 |
８ 円と接線 （略解） | |
| １ | 筑波大附属高校 （Ｒ５年） ★★★ | ４ | 大阪教育大附属平野校舎 （Ｒ４年） ★★★ |
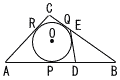 右の図のように,長さが14cmの線分AB上に点Pをとる。ただし,AP＜BPとする。(1) 線分ACの長さは,線分DEの長さの( )倍である。 【解】△ABC∽△EBD(2辺の比と夾角相等) AC＝DE×(10/5)＝2DEで, 2倍 (2) 線分ARの長さは,AR＝( )cmである。 【解】AR＝xとすると, BQ＝BP＝14−AP＝14−x…ア CQ＝CR＝8−x …イ ア＋イより,BC＝(14−x)＋(8−x)＝10で x＝AR＝6cm (3) 線分AE,CDの交点をFとするとき,AＦ:ＦEを最も簡単な整数の比で表すと,AF:FE＝( ):( )である。 【解】∠CAB＝∠DEBで,□ADECは円に内接 AF＝y,FE＝zとすると, △FAC∽△FDEより,DF＝  y△ADF∽△CEFより, y:z＝9:3で,y＝6zよって, AF:FE＝y:z＝6z:z＝6:1 |
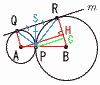 中心が点Aで半径が3cmの円と,中心が点Bで半径が6cmの円が,点Pで接している。また,2点Q,Rで2円に接するような接線をmとする。(1) QRの長さを求めなさい。 【解】（右上図参照） 垂線AHをおろすと, △ABHで,AH＝√(3＋6)2−(6−3)2＝6√2 QR＝AH＝6√2cm (2) ∠QPRの大きさを求め方も含めて答えなさい。 【解】（右上図参照） 共通接線PSを引くと,SP＝SQ＝SR ∠SPQ＝∠SQP＝x,∠SPR＝∠SRP＝yとすると, 2x＋2y＝180で,x＋y＝∠QPR＝90° (3) △QPRの面積を求めなさい。 【解】垂線PCをおろすと, △PBC∽△ABH(相似比2:3)で,BC＝3×  ＝2CR＝4で,△QPR＝ ×6√2×4＝12√2cm2 |
||
| ２ | 鎌倉学園高校 （Ｒ４年） ★★ | ５ | 埼玉県立高校 （Ｒ４年） ★★ |
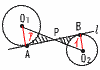 半径4cmの円O1と半径2cmの円O2があり,中心間の距離は12cmです。直線lは円O1,O2とそれぞれ点A,Bで接しています。このとき,斜線部分の面積を求めなさい。 【解】（右上図参照） △PO1Aの3辺は,8,4,4√3で,∠PO1A＝60° △PO1A＋△PO2B ＝ ×4×4√3＋×2×2√3＝10√3扇形ア＋扇形ｲ＝  (42π＋22π)＝ πよって, 10√3−  πcm2 |
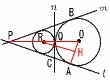 直線l,mに接し,円Ｏに点Oで接する円の中心をRとします。また,Qを通る円Oと円Rの共通の接線nとし,lとnとの交点をCとします。円Oの半径が5cm,円Rの半径が3cmであるとき,線分PCの長さを求めなさい。 【解】（右上図参照） △OPA∽△ORH(相似比3:5)より, 8:OP＝2:5で, OP＝20, PQ＝15 △ORHで, RH＝√(3＋5)2−(5−3)2＝2√15 △PCQ∽△ROHより, PC:8＝15:2√15 PC＝8×15÷2√15＝4√15cm |
||
| ３ | 駿台甲府高校 （Ｒ６年） ★★ | ６ | 鎌倉学園高校 （Ｒ６年） ★★ |
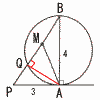 右図の半径2cmの円において,線分ABは円の直径で,直線PAは円の接線でPA＝3cmである。また,直線PBが円と交わるB以外の点をQとし,線分BQの中点をMとする。このとき,三角形APMの面積を求めよ。【解】△ＰＡＢで,PB＝5 △PAB∽△AQB(比5:4)より,QB＝  ,AQ＝ △APM＝ ×PM×AQ＝×(5−÷2)×＝102/25cm2 |
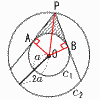 図のように中心が同じで半径がそれぞれa,2aである円C1,C2があります。C2上の点PからC1に2本の接線PA,PBを引いたとき,斜線部分の面積を求めなさい。 【解】OA＝OB＝a,OP＝2a,PA＝PB＝√3a PAOB＝2△OAP＝( ×√3a×a)×2＝√3a2斜線部分＝√3a2−  a2π＝(√3− π)a2 |
||