| 俋丂擇偮偺墌丂乮棯夝乯 | ||
| 俋丂擇偮偺墌丂乮棯夝乯 | ||
| 侾 | 嬎岝妛墍崅峑丂乮俼俆擭乯丂仛仛 | 俆 | 巗棫暉嶳崅峑丂乮俼係擭乯丂仛仛 | |||
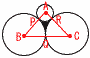 丂恾偺傛偆偵敿宎偑偦傟偧傟1,1,併2亅1偱偁傞俁偮偺墌偑奜愙偟偰偄傞丅偙偺偲偒,3偮偺墌偱埻傑傟偨恾宍偺柺愊傪媮傔傛丅 丂恾偺傛偆偵敿宎偑偦傟偧傟1,1,併2亅1偱偁傞俁偮偺墌偑奜愙偟偰偄傞丅偙偺偲偒,3偮偺墌偱埻傑傟偨恾宍偺柺愊傪媮傔傛丅亂夝亃3墌A,B,C偺愙揰傪P,Q,R偲偡傞 柺愊亖仮ABC亅(愵宍APR亄愵宍BPQ亄愵宍CQR) 丂亖 丂亖1亅 丂亖1亄( |
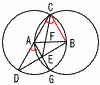 丂2揰A,B傪偦傟偧傟拞怱偲偟偰,慄暘AB傪敿宎偲偡傞墌傪偐偒,偦偺2偮偺墌偺岎揰傪C,G偲偡傞丅捈慄AC偲揰A傪拞怱偲偡傞墌偺岎揰偺偆偪,C偱偼側偄曽傪D,捈慄AG偲捈慄BD偺岎揰傪E偲偡傞丆傑偨,慄暘AB偲慄暘CE偺岎揰傪F偲偡傞丅 丂2揰A,B傪偦傟偧傟拞怱偲偟偰,慄暘AB傪敿宎偲偡傞墌傪偐偒,偦偺2偮偺墌偺岎揰傪C,G偲偡傞丅捈慄AC偲揰A傪拞怱偲偡傞墌偺岎揰偺偆偪,C偱偼側偄曽傪D,捈慄AG偲捈慄BD偺岎揰傪E偲偡傞丆傑偨,慄暘AB偲慄暘CE偺岎揰傪F偲偡傞丅(1) 仮ADE佷仮CDB傪徹柧偟側偝偄丅 亂徹柧亃 仮ABC,仮ABG偼惓嶰妏宍 仮ADE偲仮CDB偱,
(2) AF:FB傪媮傔側偝偄丅偨偩偟,嵟傕娙扨側惍悢偺斾偱昞偟側偝偄丅 亂夝亃 (1)傛傝,仮ADE佷仮CDB(憡帡斾1:2) AG//CB傛傝,仮AEF佷仮BCF(憡帡斾1:2) 傛偭偰, AF:FB亖1:2 |
|||||
| 俀 | 搶嫗岺戝晬懏壢媄崅峑丂乮俼俆擭乯丂仛仛 | |||||
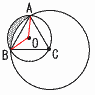 丂塭傪偮偗偨晹暘偺柺愊 丂塭傪偮偗偨晹暘偺柺愊亂夝亃 墌O偱,愵宍OAB亖(2併3)2兾亊 墌C偱,愵宍CAB亖62兾亊 塭亖(愵宍OAB亄 丂亖4兾亄 |
||||||
| 俁 | 憗堫揷嵅夑崅峑丂乮俼係擭乯丂仛仛 | 俇 | 搶奀崅峑丂乮俼係擭乯丂仛仛仛 | |||
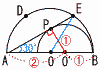 丂拞怱偑O偱慄暘AB傪捈宎偲偡傞敿墌C傪偐偒,屖AB傪3摍暘偡傞傛偆偵2揰D,E傪偲傞丅師偵,慄暘AB忋偵O'偲傝,敿宎偑O'B偱偁傞敿墌C'傪偐偔偲,C'偼慄暘AE
偵揰P偱愙偟偨丅 丂拞怱偑O偱慄暘AB傪捈宎偲偡傞敿墌C傪偐偒,屖AB傪3摍暘偡傞傛偆偵2揰D,E傪偲傞丅師偵,慄暘AB忋偵O'偲傝,敿宎偑O'B偱偁傞敿墌C'傪偐偔偲,C'偼慄暘AE
偵揰P偱愙偟偨丅(1) 佢PO'A偺戝偒偝傪媮傔傛丅 亂夝亃 佢BOE亖60亱傛傝佢A亖30亱 仮PO'A偱,佢PO'A亖90亅30亖60亱 (2) AE亖3併3偺偲偒,2偮偺敿墌偺拞怱娫偺挿偝OO' 傪媮傔傛丅 仮EBA偱,AE亖3併3傛傝,EB亖3,AB亖6 仮PAO'偱,PO':AO'亖1:2,PO'亖O'B偩偐傜, 丂AO':O'B亖2:1 OO'亖x偲偡傞偲,(3亄x):(3亅x)亖2:1 丂3亄x亖6亅2x偱, x亖OO'亖1 |
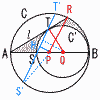 丂挿偝偑6cm偺慄暘AB傪捈宎偲偡傞墌C偲,墌C偵B偱撪愙偡傞敿宎2cm偺墌C'偑偁傞丅 丂挿偝偑6cm偺慄暘AB傪捈宎偲偡傞墌C偲,墌C偵B偱撪愙偡傞敿宎2cm偺墌C'偑偁傞丅(1) 墌C,墌C',愙慄l偱埻傑傟偨幬慄晹偼[丂丂]cm2偱偁傞丅 亂夝亃2墌偺拞怱傪P,Q偲偡傞偲, 仮AQT偱,佢A亖30亱,佢BPR亖60亱 幬慄晹亖(仮APR亄愵宍PBR)亅敿墌C' 丂亖( 丂亖 (2) 捈慄ST偲墌C偺2偮偺岎揰傪寢傫偩慄暘偺挿偝偼[丂丂]cm 仮QST偼惓嶰妏宍偱,PH亖併3亊 仮S'PT'偱,S'T'亖2S'H亖2併丂{32亅( |
|||||
| 係 | 嬎朁崅峑丂乮俼俇擭乯丂仛仛仛 | (2) AC亖5,BE亖8偺偲偒,師偺傕偺傪媮傔傛丅 嘆 仮CBF偺柺愊 亂夝亃悅慄CH傪偍傠偡偲,BH亖 仮CBF亖 嘇 EF偺挿偝 亂夝亃仮CAG佷仮GAE傛傝,CA:AG亖GA:AE 丂5:AG亖GA:18偱,AG亖3併10 仮GAE佷仮BEF傛傝,GA丗AE亖BE:EF 丂3併10:18亖8:EF偱, EF亖 嘊 仮GAE偺柺愊 亂夝亃仮GAE偼擇摍曈嶰妏宍偱,AK亖9,GK亖3 仮GAE亖 |
||||
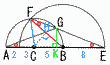 丂塃偺恾偺傛偆偵揰C傪拞怱偲偟,慄暘AB傪捈宎偲偡傞敿墌偲,揰B傪拞怱偲偟,慄暘DE傪捈宎偲偡傞敿墌偑偁傞丅 丂塃偺恾偺傛偆偵揰C傪拞怱偲偟,慄暘AB傪捈宎偲偡傞敿墌偲,揰B傪拞怱偲偟,慄暘DE傪捈宎偲偡傞敿墌偑偁傞丅丂偨偩偟,D偼慄暘AC忋偺揰偱偁傞丅 (1) GA亖GE偱偁傞偙偲傪徹柧偣傛丅 亂徹柧亃 佢A亖佢F(屖BG偺墌廃妏)乧傾 佢E亖佢F(敿宎BE亖BF)丂乧僀 傾亖僀傛傝,佢A亖佢E偱, GA亖GE 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂(塃傊偮偯偔仺) |
||||||