 図形 |
９ 二つの円 | 月 日（ ） |
| 図形 |
９ 二つの円 | 月 日（ ） |
| １ | 桐光学園高校 （Ｒ５年） ★★ | ５ | 市立福山高校 （Ｒ４年） ★★ |
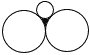 図のように半径がそれぞれ1,1,√2－1である３つの円が外接している。このとき,3つの円で囲まれた図形の面積を求めよ。 |
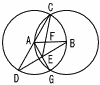 2点A,Bをそれぞれ中心として,線分ABを半径とする円をかき,その2つの円の交点をC,Gとする。直線ACと点Aを中心とする円の交点のうち,Cではない方をD,直線AGと直線BDの交点をEとする，また,線分ABと線分CEの交点をFとする。(1) △ADE∽△CDBを証明しなさい。 (2) AF:FBを求めなさい。ただし,最も簡単な整数の比で表しなさい。 |
||
| ２ | 東京工大附属科技高校 （Ｒ５年） ★★ | ||
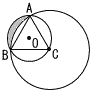 図において,3点A,B,Cは円Oの周上にあり,△ABCは1辺の長さが6cmの正三角形である。また,A,BはCを中心とする円の周上にある。このとき,影をつけた部分の面積を求めなさい。 |
|||
| ３ | 早稲田佐賀高校 （Ｒ４年） ★★ | ６ | 東海高校 （Ｒ４年） ★★★ |
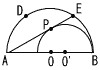 中心がOで線分ABを直径とする半円Cをかき,弧ABを3等分するように2点D,Eをとる。次に,線分AB上にO'とり,半径がO'Bである半円C'をかくと,C'は線分AE
に点Pで接した。(1) ∠PO'Aの大きさを求めよ。 (2) AE＝3√3のとき,2つの半円の中心間の長さOO' を求めよ。 |
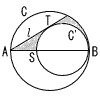 長さが6cmの線分ABを直径とする円Cと,円CにBで内接する半径2cmの円C'がある。点Aから円C'に引いた接線をl,線分ABと円C'の点B以外の共有点をS,接線lと円C'の接点をTとするとき,(1) 円C,円C',接線lで囲まれた斜線部の面積は[ ]cm2である。 (2) 直線STと円Cの2つの交点を結んだ線分の長さは[ ]cmである。 |
||
| ４ | 桐朋高校 （Ｒ６年） ★★★ | (2) AC＝5,BE＝8のとき,次のものを求めよ。 ① △CBFの面積 ② EFの長さ ③ △GAEの面積 |
|
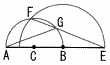 右の図のように点Ｃを中心とし,線分ABを直径とする半円と,点Ｂを中心とし,線分DEを直径とする半円がある。ただし,Dは線分AC上の点である。  と の交点をFとし,線分EFと の交点のうち,Fとは異なる点をGとする。(1) GA＝GEであることを証明せよ。 |
|||
