| �P�O�@���S�Ɠ��ډ~�@�i�����j | ||
| �P�O�@���S�Ɠ��ډ~�@�i�����j | ||
| �P | ������t���������Z�@�i�q�T�N�j�@���� | �S | ����a�w�����Z�@�i�q�S�N�j�@������ | |||||||||||||||||||||||||||||
�@��ABC�̓��ډ~�̔��a��r�Ƃ���Ƃ�,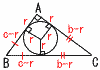 (1) r��a,b,c��p���ĕ\���B �y���z BC��a��(c�|r)�{(b�|r)���, �@r�� (2) ��ACD�̓��ډ~�̔��a��a,b,r��p���ĕ\���B �y���z ��ABC�䁢DAC���,
�y���z (2)�Ɠ��l��,��DBA�̓��ډ~�̔��a��cr/a
|
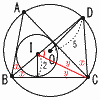 �@�_O�𒆐S�Ƃ��锼�a5�̉~��3�_A,B,C��ʂ�,�_I �𒆐S�Ƃ��锼�a2�̉~����ABC��3�ӂ��ׂĂɐڂ��Ă���B�܂�,����BI �Ɠ_O�𒆐S�Ƃ��锼�a5�̉~�Ƃ̌�_��,�_B�ƈقȂ�_��D�Ƃ���B �@�_O�𒆐S�Ƃ��锼�a5�̉~��3�_A,B,C��ʂ�,�_I �𒆐S�Ƃ��锼�a2�̉~����ABC��3�ӂ��ׂĂɐڂ��Ă���B�܂�,����BI �Ɠ_O�𒆐S�Ƃ��锼�a5�̉~�Ƃ̌�_��,�_B�ƈقȂ�_��D�Ƃ���B(1) DC��DI �ł��邱�Ƃ��ؖ�����B �@������,��IBA����IBC�c�@ �@�@�@�@ ��ICB����ICA�c�A �@�����藧���Ƃ�,�ؖ��Ȃ��ɗp���Ă��悢���̂Ƃ���B �y�ؖ��z�i�E��}�Q�Ɓj �_I�́�ABC�̓��S ��ABD����ACD��x(�~���p) ��DCI��,��DCI��x�{y�@��DIC��x�{y(�O�p) 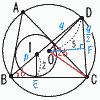 �@��DCI����DIC���, DC��DI �@��DCI����DIC���, DC��DI(2) ��IBC�̑傫����b���Ƃ���Ƃ�,��ODC�̑傫����b��p�������ŕ\���B �y���z��OCD��, ��COD��2b(���S�p) �@��ODC��(180�|2b)��2��(90�|b)�� (3) �����̒����̐� BI�DI �̒l�����߂�B �y���z��BEI�Ɓ�OFD��,��B����O��b���, �@��BEI�䁢OFD(2�p����) BI��p,DI��q�Ƃ����, 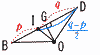 �@p:5��2: �@p:5��2:(4) ����OI �̒��������߂�B �y���z����OG�����낷��,BG��DG��, �@DG�� ��OIG�Ɓ�ODG��, �@OG2��OI2�|IG2��OD2�|DG2���, �@OI2��52�| �����,OI����5 |
|||||||||||||||||||||||||||||||
| �Q | �J�����Z�@�i�q�T�N�j�@������ | |||||||||||||||||||||||||||||||
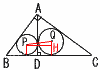
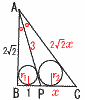 �@AB��2��2,BP��1�ł���Ƃ�, �@AB��2��2,BP��1�ł���Ƃ�,(1) AC,PC�̒��������ꂼ�ꋁ�߂�B �y���zAP�́�A�̓��� PC��x�Ƃ�����, �@2��2:AC��1:x��,AC��2��2x ��ABC��,(2��2)2�{(1�{x)2��(2��2x)2 �@�����������,x�� (2) ��PAB,��PAC�̓��ډ~�̔��a�̔�����߂�B �y���z���a��r1,r2�Ƃ����, ��ABP��,AP����(2��2)2�{12��3 �@��ABP��
|
||||||||||||||||||||||||||||||||
| �R | ���{�@��v��R���Z�@�i�q�U�N�j�@���� | �T | �a�m���{�䏗�q���Z�@�i�q�U�N�j�@�� | |||||||||||||||||||||||||||||
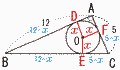 �@�E�̐}�̂悤�ȁ�A��90��,AB��12,AC��5�̒��p�O�p�`ABC������B���̎O�p�`��3�̕ӂ��ׂĂɐڂ���~�̔��a��[�@�@]�ł���B �@�E�̐}�̂悤�ȁ�A��90��,AB��12,AC��5�̒��p�O�p�`ABC������B���̎O�p�`��3�̕ӂ��ׂĂɐڂ���~�̔��a��[�@�@]�ł���B�y���z���SO����3����(���ax)�����낷 BD��BE��12�|x�c�A,�@CF��CE��5�|x�c�C �A�{�C���,(12�|x)�{(5�|x)����122�{52 �@17�|2x��13��, ���ax��2 |
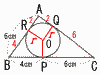 �@�E�̐}�̂悤��,��ABC�ɓ��ڂ���~������,��BC,CA,AB�Ƃ̐ړ_��,���ꂼ��P,Q,R�Ƃ���B���̂Ƃ�,���ڂ���~�̔��a�����߂�B �@�E�̐}�̂悤��,��ABC�ɓ��ڂ���~������,��BC,CA,AB�Ƃ̐ړ_��,���ꂼ��P,Q,R�Ƃ���B���̂Ƃ�,���ڂ���~�̔��a�����߂�B�y���z���SO����3����(���ar)�����낷 ��ABC��,62�{82��102�ƂȂ�,��A��90�� ��AROQ�͐����`��, ���ar��2cm |
|||||||||||||||||||||||||||||||