 図形 |
１１ 正三角形 （略解） | |
| 図形 |
１１ 正三角形 （略解） | |
| １ | 福島県立高校 （Ｒ４年） ★★ | ５ | 滋賀県立膳所高校 （Ｒ５年） ★★ | ||||||||||||||||
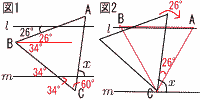 【解】(右上図参照)図1より, ∠x＝180−(34＋60) ＝180−94＝86° [別解] 図2より,△ABCを26°回転させると考えて, ∠x＝60＋26＝86° |
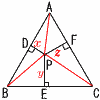 長さの和 PD＋PE＋PF が一定であることを証明し,その長さの和を求めなさい。【解】右上図参照 1辺6の△ABC＝  ×62＝9√3＝△PAB＋△PBC＋△PCA  (6x＋6y＋6z)＝9√33(x＋y＋z)＝9√3で, x＋y＋z＝3√3（一定） |
||||||||||||||||||
| ２ | 城北高校 （Ｒ５年） ★ | ６ | 城北高校 （Ｒ５年） ★★ | ||||||||||||||||
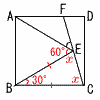 正方形ABCDの内部に正三角形を作る。∠AEFの大きさを求めよ。【解】△BCEは二等辺三角形 ∠x＝(180−30)÷2＝75° ∠AEF＝180−(60＋75)＝45° |
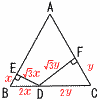 線分の長さの和 DE＋DFを求めよ。【解】△ABCの1辺をaとすると △ABC＝ a2＝√3より,a＝2BC＝2(x＋y)＝2で,x＋y＝1 よって, DE＋DF＝√3(x＋y)＝√3 |
||||||||||||||||||
| ３ | 巣鴨高校 （Ｒ４年） ★★ | ７ | 筑波大附属駒場高校 （Ｒ４年） ★★★ | ||||||||||||||||
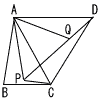 (1) △APC≡△AQDの証明【証明】 △APCと△AQDで,
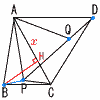 (2) △ABCの面積を求めなさい。 【解】(右図参照) 垂線BHをおろし,AH＝xとすると, △ABCで, BH2＝72−x2＝52−(8−x)2 これを解いてx＝  より, BH＝ √3△ABC＝ ×8×√3＝10√3(3) AP＋BP＋CPが最小のとき,∠APBの大きさ 【解】(1)より, AP＋BP＋CP＝PQ＋BP＋QD＝BP＋PQ＋QD ≧線分BPQD(4点が一直線のとき) ∠APB＝180−∠APQ＝180−60＝120° |
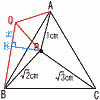 (1) 線分BQの長さ【解】 △AQB≡△APCより,BQ＝PC＝√3cm (2) △ABPと△ACPの面積の和 【解】垂線PHをおろし,QH＝xとする △PQBで,PH2＝12−x2＝(√2)2−(√3−x)2 x＝  √3より, PH＝√6△PQB＝ ×√3×√6＝√2…ア△AQP＝ ×1×√3＝ √3 …イ△ABP＋△ACP＝△ABP＋△AQB
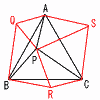 (3) 正三角形ABCの面積【解】(右図参照) 3点Q,R,Sをとって,3つの正三角形をつくる △AQB≡△APC,△BRC≡△BPA,△CSA≡△CPB さらに,△PQB≡△RCP≡△APS よって,△ABC＝六角形AQBRCS÷2 ＝[△APQ×{12＋(√2)2＋√3)2}＋△PQB×3]÷2
|
||||||||||||||||||
| ４ | 桜美林高校 （Ｒ６年） ★★★ | (2) 線分AEの長さを求めなさい。 【解】△EBDは正三角形で,ED＝6 △AEDで,AE＝√62−42＝2√5cm 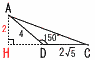 (3) △ADCの面積を求めなさい。【解】△ABD≡△ACFとなる点Fをとると, ∠ADC＝60＋90＝150°(左図の青) 右図のような△AHDを考えて,AH＝2 △ADC＝ ×2√5×2＝2√5cm2 |
|||||||||||||||||
 図のような,正三角形ABCがある。△ABCの内部に点Dを,△ABCの外部に点Eを,△BCD≡△BAE となるようにとる。AD＝4cm,BD＝6cm,∠EAD＝90°のとき, (1) ∠EBD の大きさを求めなさい。 【解】△BAE≡△BCDより,∠EBA＝∠DBC ∠EBD＝∠EBA＋∠ABD＝∠ABC＝60° (右へつづく→) |
|||||||||||||||||||
