| 11 正三角形 | 月 日( ) |
| 11 正三角形 | 月 日( ) |
| 1 | 福島県立高校 (R4年) ★★ | 5 | 滋賀県立膳所高校 (R5年) ★★ |
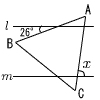 △ABCは正三角形であり,l‖mである。このとき,∠xの大きさを求めなさい。 △ABCは正三角形であり,l‖mである。このとき,∠xの大きさを求めなさい。 |
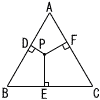 図のように,1辺の長さが6の正三角形ABCの内部にある点Pから各辺に垂線PD,PE,PFをおろす。点Pがどこにあっても,長さの和 PD+PE+PF
が一定であることを証明し,その長さの和を求めなさい。 図のように,1辺の長さが6の正三角形ABCの内部にある点Pから各辺に垂線PD,PE,PFをおろす。点Pがどこにあっても,長さの和 PD+PE+PF
が一定であることを証明し,その長さの和を求めなさい。 |
||
| 2 | 城北高校 (R5年) ★ | 6 | 城北高校 (R5年) ★★ |
 右の図のように,正方形ABCDの内部に正三角形ABEを作る。∠AEFの大きさを求めよ。 右の図のように,正方形ABCDの内部に正三角形ABEを作る。∠AEFの大きさを求めよ。 |
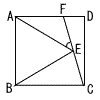
 右の図は面積が√3の正三角形ABCである。線分の長さの和 DE+DF を求めよ。 右の図は面積が√3の正三角形ABCである。線分の長さの和 DE+DF を求めよ。 |
||
| 3 | 巣鴨高校 (R4年) ★★ | 7 | 筑波大附属駒場高校 (R4年) ★★★ |
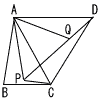 AB=7,AC=8,BC=5の△ABCがあります。図のように,△ABCの内部に点Pをとり,正三角形APQと正三角形ACDを作りました。 AB=7,AC=8,BC=5の△ABCがあります。図のように,△ABCの内部に点Pをとり,正三角形APQと正三角形ACDを作りました。(1) △APC≡△AQDを証明しなさい。 (2) △ABCの面積を求めなさい。 (3) AP+BP+CPが最小となるとき,∠APBの大きさを求めなさい。 |
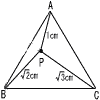 正三角形ABCの内部に点Pがあり,AP=1cm,BP=√2cm,CP=√3cmです。 正三角形ABCの内部に点Pがあり,AP=1cm,BP=√2cm,CP=√3cmです。(1) 点Qを,三角形APQが正三角形となるようにとります。ただし,線分PQと辺ABは交わります。線分BQの長さを求めなさい。 (2) △ABPと△ACPの面積の和を求めなさい。 (3) 正三角形ABCの面積を求めなさい。 |
||
| 4 | 桜美林高校 (R6年) ★★★ | (2) 線分AEの長さを求めなさい。 (3) △ADCの面積を求めなさい。 |
|
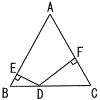
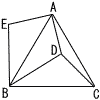 図のような,正三角形ABCがある。△ABCの内部に点Dを,△ABCの外部に点Eを,△BCD≡△BAE となるようにとる。 図のような,正三角形ABCがある。△ABCの内部に点Dを,△ABCの外部に点Eを,△BCD≡△BAE となるようにとる。AD=4cm,BD=6cm,∠EAD=90°のとき, (1) ∠EBD の大きさを求めなさい。 (右へつづく→) |
|||