 図形 |
１３ 直角三角形 （略解） | |
| 図形 |
１３ 直角三角形 （略解） | |
| １ | 千葉県立高校 （Ｒ５年） ★★★ | ５ | 城北高校 （Ｒ４年） ★★★ | |||||||||
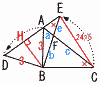 (1) 線分AEの長さを求めなさい。【解】△DBE＝△ABC＝12cm2 BH＝  で,AH＝ AE＝DE−DA＝5− ×2＝ cm(2) △ABFの面積を求めなさい。 【解】△AFE∽△BFCより,ａ:ｂ＝7:20…ア  ABCEは同一円周上で,∠AEC＝∠ABC＝90°△ACEで,CE＝24/5 △ABF∽△ECFより,b:c＝5:8…イ アイより,a:c＝(7/20)ｂ:(8/5)b＝7:32 △ABF＝△ABC×(7/39)＝6×(7/39)＝14/13cm2 |
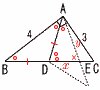 図は直角三角形でDB＝DCである。線分ADを析り目として折り返したとき,重なった部分の面積を求めよ。【解】（右図参照） △ABE∽△DAEで,DE＝x,AE＝yとすると, y:x＝4:  より,8x−5y＝0 …ア( ＋x):y＝4:より,10x−16y＝−25…イアイより, x＝DE=125/78
|
|||||||||||
| ２ | 滋賀県立高校 （Ｒ５年） ★ | ６ | 久留米大附設高校 （Ｒ４年） ★★★ | |||||||||
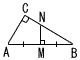 ∠C=90°の直角三角形ABCで,辺AB,CAの長さを10,5とします。(1) △ABCと△NBMの面積比を求めなさい。 【解】BC＝5√3 △ABC∽△NBM(比√3:1) 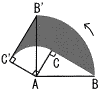 面積比＝(√3)2:12＝3:1(2) 辺BCが通過したときにできる斜線部の面積を求めなさい。 【解】(△AB'C'＋扇形ABB')−(扇形ACC'＋△ABC) ＝扇形ABB'−扇形ACC'＝102π×  −52π×＝25π−  π＝(75/4)π |
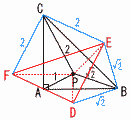 ∠A＝90°の直角二等辺三角形の内部にPA＝1,PB＝√2,PC＝2をみたす点Pをとり,点Pと辺AB,BC,CAに関して対称な点をそれぞれD,E,Fとする。(1) DE,EF,FDの長さ 【解】 △BDEは等辺√2の直角三角形で, DE＝2 △CEFは等辺2の直角三角形で, EF＝2√2 CFDEは正方形で, FD＝2(2) 五角形BECFDの面積 【解】 △BDE＋ CFDE＝ ×(√2)2＋22＝5(3) ABの長さ 【解】 △ABC＝五角形BECFD× ＝AB2＝より, AB＝√5(4) 面積比△PAB:△PBC:△PCA 【解】 (3)より,△ACPは直角三角形で,△ACP＝1 △PAB∽△PBC(3辺の比相等,1:√2) △PAB：△PBC＝12:(√2)2＝1:2 △PAB＋△PBC＝△ABC−△ACP＝ −1＝ △PAB＝ × ＝ △PBC＝× ＝1△PAB:△PBC:△PCA＝ :1:1＝1：2：2 |
|||||||||||
| ３ | 早大本庄高校 （Ｒ４年） ★★★ | |||||||||||
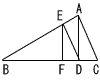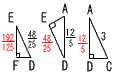 ∠ADC＝∠DEA＝∠EFD= 90°であるとき,線分EFの長さを求めよ。 【解】（右図参照）△ABC∽△DACより, AD＝AB×  ＝4×＝△ABC∽△EDAより, DE＝AB×( /5)＝4× =48/25△ABC∽△FEDより,
|
||||||||||||
| ４ | 日本大第三高校 （Ｒ６年） ★★ | (2) ECの長さを求めなさい。 【解】△ABC∽△EAC(相似比6:4＝3:2) EC＝AC× ＝4×＝ cm(3) △ADF:△ECFの面積の比を,もっとも簡単な整数の比で答えなさい。 【解】△ADC∽△EFC（相似比4:  ＝3:2)DC:FC＝3:2より,DF:FC＝1:2で,△ADF:△AFC＝1:2…ア △AECで,AF:FE＝4: ＝3:2で,△AFC:△ECF＝3:2…イアイより,△ADF:△ECF＝3:4 |
||||||||||
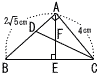 右の図のように,AB＝2√5cm,AC＝4cm,∠A＝90°の△ABCがある。∠Cの二等分線と辺ABとの交点をD,また,頂点Ａから辺BCに垂線AEを引き,CDとの交点をFとする。 (1) AD:DBの長さの比を,もっとも簡単,な整数の比で答えなさい。 【解】BC＝√(2√52)＋42＝6 CDは二等分線だから,AD:DB＝4:6＝2:3 (右へつづく→) |
||||||||||||