 図形 |
１４ 平行四辺形 （略解） | |
| 図形 |
１４ 平行四辺形 （略解） | |
| １ | 和歌山県立高校 （Ｒ５年） ★ | ４ | 専修大附属高校 （Ｒ５年） ★ | ||||||||||||||||
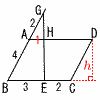 平行四辺形ABCDの辺BC上に点Eがある。 図のように,AB＝4cm,BE＝3cm,EC＝2cmのとき,辺BAの延長上にAG＝2cmとなるように点Gをとる。また,GEとADの交点をHとする。 このとき,台形ABEHの面積は,平行四辺形ABCDの面積の何倍になるか,求めなさい。 【解】  ABCDの高さをhとする△GAH∽△GBE(比1:3)より,AH＝1 台形ABEH÷ ABCD＝ (1＋3)h÷5h＝2h÷5h＝  倍 |
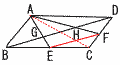 平行四辺形ABCDの面積を１とするとき,(1) AG:GEを求めなさい。 【解】Gは△ABCの重心で,AG:GE＝2:1 (2) △ABGの面積を求めなさい。 【解】△ABG＝  △ABE＝×△ABC＝ ××ABCD＝ ABCD＝ (3) △AEFの面積を求めなさい。 【解】△ABE＝△ADF＝  , △CEF＝×＝ △AEF＝1−( ＋＋)＝ |
||||||||||||||||||
| ２ | 高知県立高校 （Ｒ４年） ★★★ | ５ | 日大第二高校 （Ｒ４年） ★★★ | ||||||||||||||||
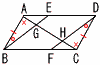 図のような,平行四辺形ABCDがある。辺AD上にAE:ED＝1:2となる点Eをとり,辺BC上に,BE‖FDとなる点Fをとる。線分ACと線分BEの交点をG,線分ACと線分FDの交点をHとする。(1) △ABG≡△CDHを証明しなさい。 【証明】 △ABE≡△CDF(2辺夾角相等9より, ∠ABE＝∠CDF …ア △ABGと△CDHで,
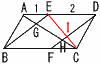 (2) 線分FDと線分CEの交点を Ｉ としたとき,平行四辺形ABCDの面積は,三角形 IHC面積の何倍か。 【解】（右図参照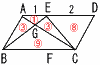）  ABCD＝Sとすると,△AEG∽△CBG(相似比1:3)より,△CEG＝(3/24)S＝ s△CIH∽△CEG(相似比1:3)より, △IHC＝ △CEG＝ ×s＝s/72で, 72倍 |
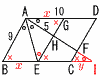 図のようにAB＝9,AD＝10の平行四辺形ABCDにおいて,(1) GHの長さを求めよ。 【解】△HAEは等辺5で,の二等辺三角形で, GH＝GE−HE＝9−5＝4 (2) AGの長さを求めよ。 【解】AG＝BE＝xとすると,△AGH∽△ABEで, AG:AB＝GH:BEより,x:9＝4:x x2−36より, x＝AG＝6 (3)  CFHEの面積は△AEHの面積の何倍になるか。【解】CI＝yとすると, △AHG∽△IHE(相似比4:5)より, I H＝  AH＝ , IE＝AG＝ △ABI∽△HEI(相似比9:5)より, (10＋y):(4＋y)＝9:5で,y＝  よって,BE:EC:CI＝AH:HF:FI＝6:4: ＝12:8:7△HEI∽△FCI(相似比15:7)より, CFHE＝{1−( )2}△IEH＝ △IEHAH:HI＝12:15＝4:5より, △AEH＝  △IEH
|
||||||||||||||||||
| ３ | 城北高校 （Ｒ６年） ★★ | ６ | 鹿児島育英館高校 （Ｒ６年） ★★ | ||||||||||||||||
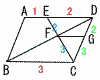 右の図の平行四辺形ＡBCDにおいて,辺AD上に点Eをとり,BDとCEの交点をＦとする。また,辺CD上にFG‖ＢBCとなるような点Gをとる。AE:ED＝1:2のとき,△DFGと△FBCの面積比を求めよ。【解】△FDE∽△FBC(相似比2:3) DG:DC＝2:5より,△DFG:△DBC＝22：52＝4:25 また,△DFG:△CFG＝2:3だから, △DFG:△FBC＝4:(25−4−6)＝4:15 |
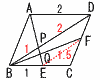 ABCDにおいて,辺BC,CDの中点をそれぞれE,Fとし,線分AEとBD,BFとの交点をそれぞれP,Qとする。(1) AP:PQ:QEを求めよ。 【解】△PAD∽PEB(相似比2:1)で,AP:PE＝2:1…ア BP＝  BD, EF＝BDで, BP：FE＝2:3△QPB∽△QEF(相似比2:3)より,PQ:QE＝2:3…イ アイより,AP:PQ:QE＝10:2:3 (2) ABCDの面積は△PBQの面積の何倍か求めよ。【解】(1)より,PQ＝  AEABCD＝4△ABE＝4×△PBQで, 30倍 |
||||||||||||||||||
