 図形 |
１４ 平行四辺形 | 月 日（ ） |
| 図形 |
１４ 平行四辺形 | 月 日（ ） |
| １ | 和歌山県立高校 （Ｒ５年） ★ | ４ | 専修大附属高校 （Ｒ５年） ★ |
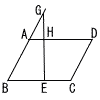 平行四辺形ABCDの辺BC上に点Eがある。ただし,辺BCの長さは辺ABの長さより長いものとする。図のように,AB＝4cm,BE＝3cm,EC＝2cmのとき,辺BAの延長上にAG＝2cmとなるように点Gをとる。また,GEとADの交点をHとする。 このとき,台形ABEHの面積は,平行四辺形ABCDの面積の何倍になるか,求めなさい。 |
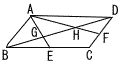 平行四辺形ABCDにおいて辺BCの中点をE,辺CDの中点をFとおく。また,直線BDと直線AEとの交点をG,直線BDと直線AFとの交点をHとおく。平行四辺形ABCDの面積を1とするとき, (1) AG:GEを求めなさい。 (2) △ABGの面積を求めなさい。 (3) △AEFの面積を求めなさい。 |
||
| ２ | 高知県立高校 （Ｒ４年） ★★★ | ５ | 日大第二高校 （Ｒ４年） ★★★ |
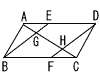 図のような,平行四辺形ABCDがある。辺AD上にAE:ED＝1:2となる点Eをとり,辺BC上に,BE‖FDとなる点Fをとる。線分ACと線分BEの交点をG,線分ACと線分FDの交点をHとする。(1) △ABG≡△CDHを証明しなさい。 (2) 線分FDと線分CEの交点をＩとしたとき,平行四辺形ABCDの面積は,三角形 IHC面積の何倍か。 |
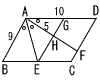 図のようにAB＝9,AD＝10の平行四辺形ABCDにおいて,∠BADの3等分線は一方が辺BCと交わり,もう一方が辺CDと交わっている。それらの交点をそれぞれE,Fとする。また,辺AD上にAB‖GEとなる点Gをとり,AFとGEの交点をHとすると,AH＝5となった。(1) GHの長さを求めよ。 (2) AGの長さを求めよ。 (3) 四角形CFHEの面積は△AEHの面積の何倍になるか求めよ。 |
||
| ３ | 城北高校 （Ｒ６年） ★★ | ６ | 鹿児島育英館高校 （Ｒ６年） ★★ |
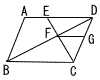 右の図の平行四辺形ABCDにおいて,辺AD上に点Eをとり,BDとCEの交点をFとする。また,辺CD上にFG‖BCとなるような点Gをとる。AE:ED＝1:2のとき,△DFGと△FBCの面積比を求めよ。 |
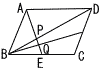  ABCDにおいて,辺BC,CDの中点をそれぞれE,Fとし,線分AEとBD,BFとの交点をそれぞれP,Qとする。(1) AP:PQ:QEを求めよ。 (2) ABCDの面積は△PBQの面積の何倍か求めよ。 |
||
