| 16 正方形 (略解) | ||
| 16 正方形 (略解) | ||
| 1 | 都立墨田川高校 (R5年) ★ | 5 | 和歌山県立高校 (R4年) ★★★ | |||
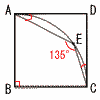 右の図において,四角形ABCDは正方形,弧ACは,頂点Bを中心とし,線分BAを半径とする円の周の一部である。 右の図において,四角形ABCDは正方形,弧ACは,頂点Bを中心とし,線分BAを半径とする円の周の一部である。弧AC上にあり,頂点A,頂点Cのいずれにも一致しない点をEとし,頂点Aと点E,頂点Cと点Eをそれぞれ結ぶ。 このとき,∠EAD+∠ECDの大きさは何度か。 【解】∠AEC=270÷2=135° ∠EAD+∠ECD=180−(∠BAD+∠BCE) =180−(360−90−135)=180−135=45° |
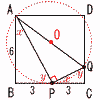 1辺が6cmの正方形ABCDの辺BC上に点P,辺CD上に点Qがある。 1辺が6cmの正方形ABCDの辺BC上に点P,辺CD上に点Qがある。BP=PC,∠BAP=∠CPQのとき,3点A,P,Qを通る円の半径を求めなさい。 【解】(右図参照) △ABP∽△PCQ(相似比2:1)で,CQ= ∠APQ=x+y=90°で,AQが円の直径 △AQDで,AQ=√{62+(6− 半径OA= |
|||||
| 2 | ラ・サール高校 (R5年) ★★★ | 6 | 大阪教育大付属平野校舎 (R4年) ★★★ | |||
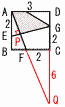 (1) 長さの比 EP:PG (1) 長さの比 EP:PG【解】Qをとると,△AEP∽△QGP EP:PG=AE:GQ=2:(2+6)=1:4 (2) 四角形APGHの面積 【解】 △AEP∽△AFB(相似比2:√10より,面積比2:5) △AEP= = |
 正方形ABCDがある。辺AB,BCの中点をそれぞれE,Fとし,CEとDFの交点をGとする。 正方形ABCDがある。辺AB,BCの中点をそれぞれE,Fとし,CEとDFの交点をGとする。(1) △CFG∽△CBEであることを証明しなさい。 【略証】 △DCF≡△CBE(2辺夾角相等)…ア △CFG∽△CBEで,
(2) 比 EG:DG:DE を求めなさい。 【解】(1)より,∠G=∠B=90° △CBEより,3辺は,1:2:√5 △CBE∽△CFG(相似比√5:1) GF=1とすると,BE=CF=√5で,EG=5−2=3 DF=DE=5より,△DEGで,DG=√52−32=4 よって, EG:DG:DE=3:4:5 |
|||||
| 3 | 城北高校 (R4年) ★★★ | |||||
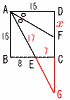 四角形ABCDは,1辺の長さが15の正方形であり,AFは∠DAEの二等分線である。このとき,DFの長さを求めよ。 四角形ABCDは,1辺の長さが15の正方形であり,AFは∠DAEの二等分線である。このとき,DFの長さを求めよ。【解】(右図参照) 延長点Gをとる △ABE∽△GDA(相似比8:15)より, DG= △AGDで,GF:DF=AG:AD= DF=xとすると,( 17x=225−8xで, x=DF=9 |
||||||
| 4 | 愛知県立高校 (R6年) ★★★ | 7 | 立命館高校 (R6年) ★★ | |||
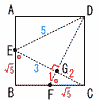
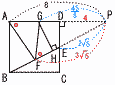 図で,四角形ABCDは正方形,Eは辺DCの中点,Fは線分EBの中点,Gは辺AD上の点で,∠GAF=∠GFEである。また,Hは線分EB上の点で,∠GHE=
90°である。AB=4cmのとき, 図で,四角形ABCDは正方形,Eは辺DCの中点,Fは線分EBの中点,Gは辺AD上の点で,∠GAF=∠GFEである。また,Hは線分EB上の点で,∠GHE=
90°である。AB=4cmのとき,(1) 線分EFの長さは[ ]cmである。 【解】△BCEで,BE=√42+22=2√5 BF= (2) 線分HFの長さは線分EBの長さの[ ]倍である。 【解】FP= △AFP∽△FGP(相似比8:3√5)より,GP= △GHP∽EDP(相似比 FH÷EB=(3√5− |
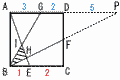 右の図の四角形ABCDは1辺の長さが10cmの正方形です。辺BC上にBE:EB=1:2となる点E,辺CD上にCF:FD=1:1となる点F,辺AD上にAG:GD=3:2となる点Gをとります。線分AEと線分BF,BGとの交点をそれぞれH,I
とするとき,△BHI の面積を求めなさい。 右の図の四角形ABCDは1辺の長さが10cmの正方形です。辺BC上にBE:EB=1:2となる点E,辺CD上にCF:FD=1:1となる点F,辺AD上にAG:GD=3:2となる点Gをとります。線分AEと線分BF,BGとの交点をそれぞれH,I
とするとき,△BHI の面積を求めなさい。【解】 AI:IE= AH:HE=2: アイより,AE:IH=14:(14−9−2)=14:3 △BHI =△ABE× |
|||||