| 19 折り返し (略解) | ||
| 19 折り返し (略解) | ||
| 1 | 青雲高校 (R5年) ★ | 4 | 城北高校 (R4年) ★★★ | ||||||||||
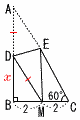 右図の直角三角形ABCにおいて,点Aが点Mに重なるように線分DEを折り目に折り返した。DBの長さを求めよ。 右図の直角三角形ABCにおいて,点Aが点Mに重なるように線分DEを折り目に折り返した。DBの長さを求めよ。【解】 AB=√3BC=4√3, AD=DM △DBMで, DB=xとおくと, x2+22=(4√3−x)2 8√3x=48−4
|
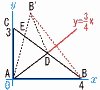 図は直角三角形でDB=DCである。線分ADを折り目として折り返したとき,重なった部分の面積を求めよ。 図は直角三角形でDB=DCである。線分ADを折り目として折り返したとき,重なった部分の面積を求めよ。【解】(右図参照)グラフを利用 BCの中点,D(2, Bの対称点B'( 直線AB'(y= 交点Eのx座標を求めると, x= △ADE:△ABC=DE:BC=(2− △ADE= |
||||||||||||
| 2 | 國學院久我山高校 (R5年) ★★ | 5 | 駿台甲府高校 (R4年) ★★★ | ||||||||||
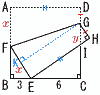 図のように,1辺が9の正方形ABCDの辺BC上にBE=3となるように点Eをとり,頂点Aが点Eに重なるように折る。折り目をFGとし,頂点Dが移った点をHとする。EHとGCの交わる点をI とするとき, 図のように,1辺が9の正方形ABCDの辺BC上にBE=3となるように点Eをとり,頂点Aが点Eに重なるように折る。折り目をFGとし,頂点Dが移った点をHとする。EHとGCの交わる点をI とするとき,(1) EFの長さを求めなさい。 【解】AF=EF=xとおくと, △FBEで, (9−x)2+32=x2 81−18x+9=0より, EF=x=5 (2) CI の長さを求めなさい。 【解】BF=9−5=4 △CIE∽△BEFより, CI:3=6:4で, CI= (3) GI の長さを求めなさい。 【解】GI=yとおくと,GH= △GIH∽△EIC∽△FEBより, y:5=( (4) GFの長さを求めなさい。 【解】GからEFに垂線GKをおろすと, GK=HE=DA=9 KE=GH=GD=2より,FK=5−2=3 △GFKで, GF=√32+92=3√10 |
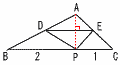 BC=3cmの△ABCにおいて,BP:PC=2:1となる点Pを辺BC上にとる。 BC=3cmの△ABCにおいて,BP:PC=2:1となる点Pを辺BC上にとる。右図のように,点AがPに重なるようにDEで折り曲げるとき, (1) DE‖BCのとき,△PDEの面積は△ABCの面積の何倍になるか。 【解】D,Eは中点 △PDE∽△ABC(相似比1:2)より, 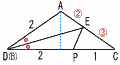 (2) △ABCがAB=ACの二等辺二角形で,点Dが頂点Bと一致するとき,△PDEの面積を求めよ。 (2) △ABCがAB=ACの二等辺二角形で,点Dが頂点Bと一致するとき,△PDEの面積を求めよ。【解】AE:CE=DA:DC=2:3 △PDE= 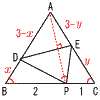 (3) △ABCが正三角形のとき,△PDEの面積を求めよ。 (3) △ABCが正三角形のとき,△PDEの面積を求めよ。【解】 △PBD∽△ECPより, 2:x:(3−x)=y:1:(3−y) これを解いて,x= AD:DB=7:5 AE:EC=7:8より, △PDE=△ADE=△ABC×
|
||||||||||||
| 3 | 西大和学園高校 (R6年) ★★ | 6 | 灘 高校 (R6年) ★★★ | ||||||||||
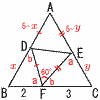 図のように,一辺の長さが5の正三角形ABCがあり,辺AB,AC上に点D,Eを とる。線分DEを折り目にして三角形ADEを折ると,点Aは辺BC上の点Fに移っ
た。BF=2のとき,線分BDと線分CEの長さの積BD×CEは[ ]であり,BDは[ ] である。 図のように,一辺の長さが5の正三角形ABCがあり,辺AB,AC上に点D,Eを とる。線分DEを折り目にして三角形ADEを折ると,点Aは辺BC上の点Fに移っ
た。BF=2のとき,線分BDと線分CEの長さの積BD×CEは[ ]であり,BDは[ ] である。【解】a+b=120° △BFD∽△CEFより,x:3=2:y=(5−x):(5−y) x:3=2:yで,xy=BD×CE=6 …ア x:(5−x)=3:(5−y)で,15−3x=5x−xy…イ アをイに代入して,x=AD=21/8 |
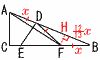 AC=5,BC=12,∠C=90°である直角三角形ABCにおいて,辺AB上の点と辺BC上の点Eを通る直線を折り目としてこの三角形を折ったとき,頂点Aが辺BC上.の点Fと重なり,AD=BFとなった。.このとき,線分BFの長さは[ ]である。 AC=5,BC=12,∠C=90°である直角三角形ABCにおいて,辺AB上の点と辺BC上の点Eを通る直線を折り目としてこの三角形を折ったとき,頂点Aが辺BC上.の点Fと重なり,AD=BFとなった。.このとき,線分BFの長さは[ ]である。【解】AD=DF=BF=xとする AB=√52+122=13 △BFDは二等辺三角形で,垂線FHをおろすと,BH=DH △BFH∽△BACより,BH= AB=x+ |
||||||||||||