 図形 |
２０ 半円 ・ 扇形 （略解） | |
| 図形 |
２０ 半円 ・ 扇形 （略解） | |
| １ | 西大和学園高校 （Ｒ５年） ★★ | ４ | 中央大附属横浜高校 （Ｒ５年） ★★ |
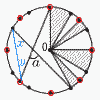 図は中心がOで半径が4の円周上に,円周を8等分する点と12等分する点を描いたものである。点が重複しているものもある。図の斜線部分の面積は(あ )である。また,図の角aの大きさは(い )°である。【解】 8等分点(45°の扇形), 12等分点(30°の扇形) 斜線部分(扇形の合計)は90° あ＝42π×＝4π ∠xは円周の5/24で,∠x＝360×(5/24)÷2=75/2 ∠yは円周の  で,∠y＝360×÷2=30い＝∠a＝(75/2)＋30＝135/2 (67.5) |
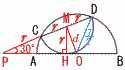 図のように,ABを直径とする半径７の半円の内側に,CDを直径とする半径rの半円が内接している。(1) 直径ABの中点と直径CDの中点の距離をdとするとき,r/dの値を求めなさい。 【解】PH＝√3r △MPH∽△OPMより,r:d＝√3r:2rで,r/d＝  (2) rの値を求めなさい。 【解】△ODMで r2＋d2＝r2＋(  √3r)2＝( )2より, r＝√21/2 |
||
| ２ | 明大付属明治高校 （Ｒ４年） ★★★ | ５ | 筑波大附属高校 （Ｒ４年） ★★★ |
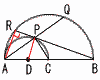 図のように,長さ8の線分ABを直径とする半円Cがあり,線分ACを直径とする半円Dがある。(1) 線分BRの長さを求めよ。 【解】 △BPD∽△BRA(相似比3:4)より,AR＝2×  ＝ △ABRで, BR＝√ {82−( )2}＝ √2(2) 線分APの長さを求めよ。 【解】 △BPDで,BP＝√62−22＝4√2 PR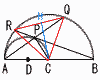＝  √2−4√2＝√2△APRで,AP＝√ {( √2)2＋()2}＝ √6 (3) △CQRの面積を求めよ。【解】（右図参照） △PQR∽△PBA(相似比1:√3)より, QR＝8×  ＝√3△CQRで垂線CHをおろすと, CH＝√ {42−( √3)2}＝√6△CQR＝  ×√3×√6＝√2 |
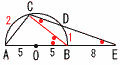 線分ABを直径とする半円Oの 上に, ＝2 となるような2点C,Dをとり,直線AB,CDの交点をEとする。AB＝10cm,BE＝8cmであるとき, (1) 線分BCの長さは,BC＝[ ]cmである。 【解】 △BCEで,BC＝BE＝8cm 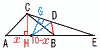 (2) 線分BDの長さは,BD＝[ ]cmである。【解】△ABCで,AH＝xとすると, CH2＝62−x2＝82−(10−x)2より,x＝  CH＝√ {62−( )2}＝ △CHEで,CE＝√ {(  )2＋()2}＝√10△BDE∽△CAEより, BD＝48÷ √10＝√10cm(3) △OCDの面積は,[ ]cm2である。 【解】（右上図参照） △BDE∽△CAEより, DE＝18× √10＝3√10CD＝ √10−3√10＝ √10△ODGで,OG＝√ {52−(  √10)2}＝ √10△OCD＝ ×√10×√10＝117/10cm2 |
||
| ３ | 青山学院高等部 （Ｒ６年） ★★★ | ６ | 桐光高校 （Ｒ６年） ★★ |
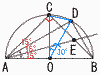 AB＝6cm,BD＝3cmのとき,(1) 線分AEの長さを求めよ． 【解】△ACEで,AC＝3√2,∠AEC＝60° AE＝  AC＝×3√2＝2√6cm(2) 線分BEの長さを求めよ． 【解】BE＝CB−CE＝3√2− 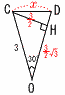AE＝(3√2−√6)cm (3) 線分CDの長さを求めよ．【解】△OCDは頂角30°の二等辺三角形 △CDHで,x2＝(  )2＋(3−√3)2＝18−9√3x2＝  (4−2√3)＝(√3−1)2で,x＝CD＝  (√6−√2)cm |
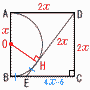 図のように,正方形ABCDの辺ABを直径とする半円と,頂点Dと辺BC上の点Eを結んだ線分が接している。線分DEの長さが6cmのとき,半円の面積を求めよ。【解】半円の半径をxとすると, DA＝DH＝DC＝2x EB＝EH＝6−2x EC＝BC−BE＝2x−(6−2x)＝4x−6 △DECで,(2x)2＋(4x−6)2＝62 4x(5x−12)＝0で,x＝  半円＝( )2π×＝(72/25)πcm2 |
||